Optimally selecting the top k values from X + Y with layer-ordered heaps

Naive approach

Top-k can be solved trivially in $O(n^2\log (n)+k)=O(n^2\log (n))$ steps by generating and sorting all n² values of the form X_i + Y_j. By using median-of-medians (Blum et al., 1973), this can be improved to O(n²) steps by generating all n² values and performing k-selection on them.

Existing, tree-based methods for top-k

In 1982, Frederickson & Johnson introduced a method reminiscent of median-of-medians (Blum et al., 1973); their method selects only the k ^th minimum value from X + Y in $O(n+min(n,k)\log \left({\displaystyle \frac{k}{min(n,k)}}\right))$ steps (Frederickson & Johnson, 1982).

Frederickson subsequently published a second algorithm, which finds the k smallest elements from a min-heap in O(k), assuming the heap has already been built (Frederickson, 1993). Combining this method with a combinatoric heap on X + Y (described below for the Kaplan et al. method) solves top-k in O(n + k). The tree data structure in Frederickson’s method can be combined with a combinatoric heap to compute the k^th smallest value from X + Y.

Kaplan et al. described an alternative method for selecting the k^th smallest value (Kaplan et al., 2019); that method explicitly used Chazelle’s soft heaps (Chazelle, 2000). By heapifying X and Y in linear time (i.e., guaranteeing w.l.o.g. that $X_i\le X_{2i},X_{2i+1}$), min_i,j X_i + Y_j = X₁ + Y₁. Likewise, $X_i+Y_j\le X_{2i}+Y_j,X_{2i+1}+Y_j,X_i+Y_{2j},X_i+Y_{2j+1}$. The soft heap is initialized to contain tuple (X₁ + Y₁,1,1). Then, as tuple (v,i,j) is popped from soft heap, lower-quality tuples are inserted into the soft heap. These lower-quality tuples of (i,j) are

(1) $$\{\begin{array}{cc}\{(2i,1),(2i+1,1),(i,2),(i,3)\},& j=1\\ \{(i,2j),(i,2j+1)\},& j>1.\\ & \end{array}$$

In the matrix X_i + Y_j (which is not realized), this scheme progresses in row-major order, thereby avoiding a tuple being added multiple times.

To compute the k^th smallest value from X + Y, the best k values are popped from the soft heap. Even though only the minimal k values are desired, “corruption” in the soft heap means that the soft heap will not always pop the minimal value; however, as a result, soft heaps can run faster than the $\mathrm{\Omega }(n\log (n))$ lower bound on comparison sorting. The free parameter $\epsilon \in (0,{\displaystyle \frac{1}{2}]}$ bounds the number of corrupt elements in the soft heap (which may be promoted earlier in the queue than they should be) as ≤ t · ε, where t is the number of insertions into the soft heap thus far. Thus, instead of popping k items (and inserting their lower-quality dependents as described in Eq. (1)), the total number of pops, p, can be found: The maximal size of the soft heap after p pops is ≤ 3p (because each pop removes one element and inserts ≤ 4 elements according to Eq. (1)); therefore, p − corruption ≥ p − 4p· ε, and thus $p-4p\cdot \epsilon \ge k$ guarantees that $p-corruption\ge k$. This leads to $p={\displaystyle \frac{k}{1-4\epsilon }}$, $\epsilon \le {\displaystyle \frac{1}{4}}$. This guarantees that Θ(k) values, which must include the minimal k values, are popped. These values are post-processed to retrieve the minimal k values via linear time one-dimensional selection (Blum et al., 1973). For constant ε, both pop and insertion operations to the soft heap are $\in \tilde{O}(1)$, and thus the overall runtime of the algorithm is ∈ O(n + k).

Note that the Kaplan et al. method easily solves top-k in O(n + k) steps; this is because computing the k^th smallest value from X + Y pops the minimal k values from the soft heap.

Layer-ordered heaps and a novel selection algorithm on X + Y

This paper uses layer-ordered heaps (LOHs) (Kreitzberg et al., 2020) to produce an optimal selection algorithm on X + Y. LOHs are stricter than heaps but not as strict as sorting: Heaps guarantee only that X_i ≤ X_children(i), but do not guarantee any ordering between one child of X_i, a, and the child of the sibling of a. Sorting is stricter still, but sorting n values cannot be done faster than ${\log }_2(n!)\in \mathrm{\Omega }(n\log (n))$. LOHs partition the array into several layers such that the values in a layer are ≤ to the values in subsequent layers: X^(u) = X^(u)₁, X^(u)₂, … ≤ X^{(u + 1)}. The size of these layers starts with |X⁽¹⁾| = 1 and grows exponentially such that $\underset{u\to \mathrm{\infty }}{lim}{\displaystyle \frac{|X^{(u+1)}|}{|X^{(u)}|}=\alpha \ge 1}$ (note that α = 1 is equivalent to sorting because all layers have size 1). By assigning values in layer u children from layer u + 1, this can be seen as a more constrained form of the heap; however, unlike sorting, for any constant α > 1, LOHs can be constructed ∈ O(n) by performing iterative linear time one-dimensional selection, iteratively selecting and removing the largest layer until all layers have been partitioned. For example, 8,1,6,4,5,3,2 can be LOHified with α = 2 into an LOH with three layers (1 ≤ 3,2 ≤ 8,4,6,5) by first selecting the largest 4 values on the entire list (8,4,6,5), removing them, and then selecting the largest 2 values from the remaining 3 values (3,2).

Although selections reminiscent of LOHs may have been used previously, formalization of rank α LOHs has been necessary to demonstrate that for $1\ll \alpha \ll 2$, a combination of LOHs and soft heaps allow generating the minimum k values from X₁ + X₂ + ⋯ + X_m (where each X_i has length n) in $o(n\cdot m+k\cdot m)$ (Kreitzberg, Lucke & Serang, 2020). Furthermore, efficiently constructing an LOH of rank α is not trivial when $\alpha \ll 2$; after all, $\alpha \to 1$ results in layers of size |X⁽¹⁾| = |X⁽²⁾| = ⋯ = 1, indicating a sorting, which implies a runtime ∈ Ω(nlog(n)) (Pennington et al., 2020).

A python implementation of a LOH is shown in listing 1.

Contribution in this manuscript

The new, optimal algorithm for solving top-k presented here makes extensive use of LOHs. It is simple to implement, does not rely on anything more complicated than linear time one-dimensional selection (i.e., it does not use soft heap). Due to its simplicity and contiguous memory access, it has a fast performance in practice.

Algorithm

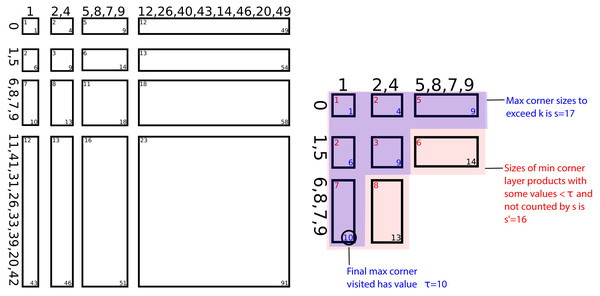
The algorithm presented is broken into phases. An illustration of these phases is provided in Fig. 1.

Proof of correctness

Lemma 2.4 proves that at termination all layer products found in q must contain the minimal k values in X + Y. Thus, by performing one-dimensional k-selection on those values in phase 3, the minimal k values in X + Y are found.

Lemma 2.1. If $\lfloor (u,v)\rfloor$ is popped from H, then both $\lfloor (u-1,v)\rfloor$ (if u > 1) and $\lfloor (u,v-1)\rfloor$ (if v > 1) must previously have been popped from H.

Proof. There is a chain of pops and insertions backwards from $\lfloor (u,v)\rfloor$ to $\lfloor (1,1)\rfloor$.

When both u, v = 1, the lemma is true.

W.l.o.g. if u = 1 this chain is of the form $\lfloor (1,1)\rfloor ,\dots ,\lfloor (1,2)\rfloor ,\dots \lfloor (1,3)\rfloor ,\dots \lfloor (u,v)\rfloor$, proving the lemma for that case.

Otherwise, both $u,v>1$. Because insertions into H increment either row or column, something of the form $\lfloor (a,v-1)\rfloor$ with $a\le u$ must be inserted into H before inserting $\lfloor (u,v)\rfloor$. $\lfloor (a,v-1)\rfloor <\lfloor (u,v)\rfloor$, so $\lfloor (a,v-1)\rfloor$ must precede $\lfloor (u,v)\rfloor$ in the chain of pops. If a = u, then $\lfloor (u,v-1)\rfloor$ is popped before $\lfloor (u,v)\rfloor$. If a < u, then from the insertion of $\lfloor (a,v-1)\rfloor$ into H, until $\lfloor (u,v-1)\rfloor$ is popped, H must contain something of the form $\lfloor (a^{\prime },v-1)\rfloor :a^{\prime }\le u$, because popping $\lfloor (a^{\prime },v-1)\rfloor$ inserts $\lfloor (a^{\prime }+1,v-1)\rfloor$. $\lfloor (a^{\prime },v-1)\rfloor <\lfloor (u,v)\rfloor$ when $a^{\prime }\le u$; therefore, $\lfloor (u,v)\rfloor$ cannot be popped before any $\lfloor (a^{\prime },v-1)\rfloor$ currently in H. Because there are a finite number of these a' and they are not revisited, before $\lfloor (u,v)\rfloor$ is popped, $\lfloor (u,v-1)\rfloor$ must be popped. This same process can be repeated with $\lfloor (u-1,b)\rfloor :b\le v$ to show that $\lfloor (u-1,v)\rfloor$ must be popped before $\lfloor (u,v)\rfloor$, proving the lemma for the final case. □

Lemma 2.2 If $\lceil (u,v)\rceil$ is popped from H, then both $\lceil (u-1,v)\rceil$ (if u>1) and $\lceil (u,v-1)\rceil$ (if v > 1) must previously have been popped from H.

Proof. Inserting $\lceil (u,v)\rceil$ requires previously popping $\lfloor (u,v)\rfloor$. By lemma 2.1, this requires previously popping $\lfloor (u-1,v)\rfloor$ (if u > 1) and $\lfloor (u,v-1)\rfloor$ (if v > 1). These pops will insert $\lceil (u-1,v)\rceil$ and $\lceil (u,v-1)\rceil$ respectively. Thus, $\lceil (u-1,v)\rceil$ and $\lceil (u,v-1)\rceil$, which are both $<\lceil (u,v)\rceil$, are inserted before $\lceil (u,v)\rceil$, and will therefore be popped before $\lceil (u,v)\rceil$. □

Lemma 2.3 All tuples will be visited in ascending order as they are popped from H.

Proof. Let $\lfloor (u,v)\rfloor$ be popped from H and let $\lfloor (a,b)\rfloor <\lfloor (u,v)\rfloor$. Either w.l.o.g. a < u, b ≤ v, or w.l.o.g. a < u, b > v. In the former case, $\lfloor (a,b)\rfloor$ will be popped before $\lfloor (u,v)\rfloor$ by applying induction to lemma 2.1.

In the latter case, lemma 2.1 says that $\lfloor (a,v)\rfloor$ is popped before $\lfloor (u,v)\rfloor$. $\lfloor (a,v)\rfloor <\lfloor (a,v+1)\rfloor <\lfloor (a,v+1)\rfloor <\cdots <\lfloor (a,b)\rfloor <\lfloor (u,v)\rfloor$, meaning that $\mathrm{\forall }r\in [v,b],\lfloor (a,r)\rfloor <\lfloor (u,v)\rfloor$. After $\lfloor (a,v)\rfloor$ is inserted (necessarily before it is popped), at least one such $\lfloor (a,r)\rfloor$ must be in H until $\lfloor (a,b)\rfloor$ is popped. Thus, all such $\lfloor (a,r)\rfloor$ will be popped before $\lfloor (u,v)\rfloor$.

Ordering on popping with $\lceil (a,b)\rceil <\lceil (u,v)\rceil$ is shown in the same manner: For $\lceil (u,v)\rceil$ to be in H, $\lfloor (u,v)\rfloor$ must have previously been popped. As above, whenever $\lceil (u,v)\rceil$ is in H, then $\lfloor (a,v)\rfloor$ must have been popped, inserting $\lfloor (a,v+1)\rfloor$ into H. Each $\lfloor (a,r)\rfloor$ popped inserts

$\lfloor (a,r+1)\rfloor$, so at least one $\lfloor (a,r)\rfloor ,r\in [v,b]$ must also be in H until $\lfloor (a,b)\rfloor$ is popped. These $\lfloor (a,r)\rfloor \le \lfloor (a,b)\rfloor <\lceil (a,b)\rceil <\lceil (u,v)\rceil$, and so $\lceil (a,b)\rceil$ will be popped before $\lceil (u,v)\rceil$.

Identical reasoning also shows that $\lfloor (a,b)\rfloor$ will pop before $\lceil (u,v)\rceil$ if $\lfloor (a,b)\rfloor <\lceil (u,v)\rceil$ or if $\lceil (a,b)\rceil <\lfloor (u,v)\rfloor$.

Thus, all tuples are popped in ascending order. □

Lemma 2.4 At the end of phase 2, the layer products whose indices are found in q contain the minimal k values.

Proof. Let (u,v) be the layer product that first makes s≥ k. There are at least k values of X + Y that are $\le max(X^{(u)}+Y^{(v)})$; this means that $\tau =max(select(X+Y,k))\le max(X^{(u)}+Y^{(v)})$. The quality of the elements in layer products in q at the end of phase 1 can only be improved by trading some value for a smaller value, and thus require a new value <max(X^(u) + Y^(v)).

By lemma 2.3, tuples will be popped from H in ascending order; therefore, any layer product $(u^{\prime },v^{\prime })$ containing values $<max(X^{(u)}+Y^{(v)})$ must have had $\lfloor (u^{\prime },v^{\prime })\rfloor$ popped before $\lceil (u,v)\rceil$. If $\lceil (u^{\prime },v^{\prime })\rceil$ was also popped, then this layer product is already included in q and cannot improve it. Thus the only layers that need be considered further have had $\lfloor (u^{\prime },v^{\prime })\rfloor$ popped but not $\lceil (u^{\prime },v^{\prime })\rceil$ popped; these can be found by looking for all $\lceil (u^{\prime },v^{\prime })\rceil$ that have been inserted into H but not yet popped.

Phase 2 appends to q all such remaining layer products of interest. Thus, at the end of phase 2, q contains all layer products that will be represented in the k-selection of X + Y. □

A python implementation of this method is shown in listing 2.

Runtime

Theorem 2.8 proves that the total runtime is ∈ O(n + k).

Lemma 2.5 Let (u′,v′) be a layer product appended to q during phase 2. Either u′ = 1, v′ = 1, or (u′ − 1,v′ − 1) was already appended to q in phase 1.

Proof. Let u′>1 and v′>1. By lemma 2.3, minimum and maximum layer products are popped in ascending order. By the layer ordering property of X and Y, $max(X^{(u^{\prime }-1)})\le min(X^{(u^{\prime })})$ and $max(Y^{(v^{\prime }-1)})\le min(Y^{(v^{\prime })})$. Thus, $\lceil (u^{\prime }-1,v^{\prime }-1)\rceil <\lfloor (u^{\prime },v^{\prime })\rfloor$ and so $\lceil (u^{\prime }-1,v^{\prime }-1)\rceil$ must be popped before $\lfloor (u^{\prime },v^{\prime })\rfloor$. □

Lemma 2.6 s, the number of elements in all layer products appended to q in phase 1, is ∈ O(k).

Proof. (u,v) is the layer product whose inclusion during phase 1 in q achieves s ≥ k; therefore, $s-|X^{(u)}+Y^{(v)}|<k$. This happens when $\lceil (u,v)\rceil$ is popped from H.

If k = 1, popping $\lceil (1,1)\rceil$ ends phase 1 with s = 1 ∈ O(k).

If k > 1, then at least one layer index is >1: u > 1 or v > 1. W.l.o.g., let u > 1. By lemma 2.1, popping $\lceil (u,v)\rceil$ from H requires previously popping $\lceil (u-1,v)\rceil$. $|X^{(u)}+Y^{(v)}|=|X^{(u)}|\cdot |Y^{(v)}|\approx \alpha \cdot |X^{(u-1)}|\cdot |Y^{(v)}|=\alpha \cdot |X^{(u-1)}+Y^{(v)}|$ (where ≈ indicates asymptotic behavior); therefore, |X^(u) + Y^(v)|∈ O(|X^{(u − 1)} + Y^(v)|). |X^{(u − 1)} + Y^(v)| is already counted in s − |X^(u) + Y^(v)| < k, and so $|X^{(u-1)}+Y^{(v)}|<k$ and |X^(u) + Y^(v)|∈ O(k). $s<k+|X^{(u)}+Y^{(v)}|\in O(k)$ and hence s ∈ O(k). □

Lemma 2.7 s′, the total number of elements in all layer products appended to q in phase 2, ∈ O(k).

Proof. Each layer product appended to q in phase 2 has had $\lfloor (u^{\prime },v^{\prime })\rfloor$ popped in phase 1. By lemma 2.5, either u′ = 1 or v′ = 1 or $\lceil (u^{\prime }-1,v^{\prime }-1)\rceil$ must have been popped before $\lfloor (u^{\prime },v^{\prime })\rfloor$.

First consider when u′ > 1 and v′ > 1. Each (u′,v′) matches exactly one layer product (u′ − 1,v′ − 1). Because $\lceil (u^{\prime }-1,v^{\prime }-1)\rceil$ must have been popped before $\lfloor (u^{\prime },v^{\prime })\rfloor$, then $\lceil (u^{\prime }-1,v^{\prime }-1)\rceil$ was also popped during phase 1. s, the count of all elements whose layer products were inserted into q in phase 1, includes $|X^{(u^{\mathrm{\prime }}-1)}+Y^{(v^{\mathrm{\prime }}-1)}|$ but does not include X^(u′) + Y^(v′) (the latter is appended to q during phase 2). By exponential growth of layers in X and Y, $|X^{(u^{\mathrm{\prime }})}+Y^{(v^{\mathrm{\prime }})}|\approx {\alpha }^2\cdot |X^{(u^{\mathrm{\prime }}-1)}+Y^{(v^{\mathrm{\prime }}-1)}|$. These |X^{(u′ − 1)} + Y^{(v′ − 1)}| values were included in s during phase 1, and thus the total number of elements in all such (u′ − 1,v′ − 1) layer products is ≤ s. Thus the sum of sizes of all layer products (u′,v′) with u′ > 1 and v′ > 1 that are appended to q during phase 2 is asymptotically ≤ α²· s.

When either u′ = 1 or v′ = 1, the number of elements in all layer products must be ∈ O(n): ${\sum }_{u^{\mathrm{\prime }}}|X^{(u^{\mathrm{\prime }})}+Y^{(1)}|+{\sum }_{v^{\mathrm{\prime }}}|X^{(u^{\mathrm{\prime }})}+Y^{(1)}|<2n$; however, it is possible to show that contributions where u′ = 1 or v′ = 1 are ∈ O(k):

W.l.o.g. for u′>1, $\lfloor (u\prime ,1)\rfloor$ is inserted into H only when $\lfloor (u\prime -1,1)\rfloor$ is popped. Thus at most one $\lfloor (u\prime ,1)\rfloor$ can exist in H at any time. Furthermore, popping $\lfloor (u\prime ,1)\rfloor$ from H requires previously popping $\lceil (u\prime -1,1)\rceil$ from H: layer ordering on X implies max(X^{(u′ − 1)}) ≤ min (X^(u′)) and |Y⁽¹⁾| = 1 implies min(Y⁽¹⁾) = max(Y⁽¹⁾), and so $\lceil (u^{\mathrm{\prime }}-1,1)\rceil =(max(X^{(u^{\mathrm{\prime }}-1)}+Y^{(1)}),(u^{\mathrm{\prime }}-1,1),1)<\lfloor (u^{\mathrm{\prime }},1)\rfloor =(min(X^{(u^{\mathrm{\prime }})}+Y^{(1)}),(u^{\mathrm{\prime }},1),0)$. Thus $\lceil (u\prime -1,1)\rceil$ has been popped from H and counted in s. By the exponential growth of layers, the contribution of all such u′ > 1, v′ = 1 will be $\approx \le \alpha \cdot s$, and so the contributions of u′ > 1, v′ = 1 or u′ = 1, v′ > 1 will be ≈ ≤ 2 α · s.

When u′ = v′ = 1, the layer product contains 1 element.

Therefore, s′, the total number of elements found in layer products appended to q during phase 2, has $s^{\mathrm{\prime }}\le ({\alpha }^2+2\alpha )\cdot s+1$. By lemma 2.6, $s\in O(k)$, and thus s′∈ O(k). □

Theorem 2.8 The total runtime of the algorithm is ∈ O(n + k).

Proof. For any constant α > 1, LOHification of X and Y runs in linear time, and so phase 0 runs ∈ O(n).

The total number of layers in each LOH is ≈ log_α(n); therefore, the total number of layer products is $\approx {\log }_{\alpha }^2(n)$. In the worst-case scenario, the heap insertions and pops (and corresponding set insertions and removals) will sort ≈ 2 log²_α(n) elements, because each layer product may be inserted as both $\lfloor ·\rfloor$ or $\lceil ·\rceil$; the worst-case runtime via comparison sort will be $\in O({\log }_{\alpha }^2(n)\log ({\log }_{\alpha }^2(n)))\subset o(n)$. The operations to maintain a set of indices in the heap have the same runtime per operation as those inserting/removing to a binary heap, and so can be amortized out. Thus, the runtimes of phases 1–2 are amortized out by the O(n) runtime of phase 0.

Lemma 2.6 shows that s∈ O(k). Likewise, lemma 2.7 shows that s′∈ O(k). The number of elements in all layer products in q during phase 3 is s + s′∈ O(k). Thus, the number of elements on which the one-dimensional selection is performed will be $\in O(k)$. Using a linear time one-dimensional selection algorithm, the runtime of the k-selection in phase 3 is ∈ O(k).

The total runtime of all phases ∈ O(n + k + k + k) = O(n + k). □

Python code

Listing 1. LayerOrderedHeap.py: A class for LOHifying, retrieving layers, and the minimum and maximum value in a layer.

# https://stackoverflow.com/questions/10806303/python-implementation-of-median-of-medians-algorithm

def median_of_medians_select(L, j): # returns j-th smallest value:

if len(L) < 10:

L.sort()

return L[j]

S = []

lIndex = 0

while lIndex+5 < len(L)-1:

S.append(L[lIndex:lIndex+5])

lIndex += 5

S.append(L[lIndex:])

Meds = []

for subList in S:

Meds.append(median_of_medians_select(subList, int((len(subList)-1)/2)))

med = median_of_medians_select(Meds, int((len(Meds)-1)/2))

L1 = []

L2 = []

L3 = []

for i in L:

if i < med:

L1.append(i)

elif i > med:

L3.append(i)

else:

L2.append(i)

if j < len(L1):

return median_of_medians_select(L1, j)

elif j < len(L2) + len(L1):

return L2[0]

else:

return median_of_medians_select(L3, j-len(L1)-len(L2))

def partition(array, left_n):

n = len(array)

right_n = n - left_n

# median_of_medians_select argument is index, not size:

max_value_in_left = median_of_medians_select(array, left_n-1)

left = []

right = []

for i in range(n):

if array[i] < max_value_in_left:

left.append(array[i])

elif array[i] > max_value_in_left:

right.append(array[i])

num_at_threshold_in_left = left_n - len(left)

left.extend([max_value_in_left]*num_at_threshold_in_left)

num_at_threshold_in_right = right_n - len(right)

right.extend([max_value_in_left]*num_at_threshold_in_right)

return left, right

def layer_order_heapify_alpha_eq_2(array):

n = len(array)

if n == 0:

return []

if n == 1:

return array

new_layer_size = 1

layer_sizes = []

remaining_n = n

while remaining_n > 0:

if remaining_n >= new_layer_size:

layer_sizes.append(new_layer_size)

else:

layer_sizes.append(remaining_n)

remaining_n -= new_layer_size

new_layer_size *= 2

result = []

for i,ls in enumerate(layer_sizes[::-1]):

small_vals,large_vals = partition(array, len(array) - ls)

array = small_vals

result.append(large_vals)

return result[::-1]

class LayerOrderedHeap:

def __init__(self, array):

self._layers = layer_order_heapify_alpha_eq_2(array)

self._min_in_layers = [ min(layer) for layer in self._layers ]

self._max_in_layers = [ max(layer) for layer in self._layers ]

#self._verify()

def __len__(self):

return len(self._layers)

def _verify(self):

for i in range(len(self)-1):

assert(self.max(i) <= self.min(i+1))

def __getitem__(self, layer_num):

return self._layers[layer_num]

def min(self, layer_num):

assert( layer_num < len(self) )

return self._min_in_layers[layer_num]

def max(self, layer_num):

assert( layer_num < len(self) )

return self._max_in_layers[layer_num]

def __str__(self):

return str(self._layers)

Listing 2. CartesianSumSelection.py: A class for efficiently performing selection on X + Y in Θ(n + k) steps.

from LayerOrderedHeap import *

import heapq

class CartesianSumSelection:

def _min_tuple(self,i,j):

# True for min corner, False for max corner

return (self._loh_a.min(i) + self._loh_b.min(j), (i,j), False)

def _max_tuple(self,i,j):

# True for min corner, False for max corner

return (self._loh_a.max(i) + self._loh_b.max(j), (i,j), True)

def _in_bounds(self,i,j):

return i < len(self._loh_a) and j < len(self._loh_b)

def _insert_min_if_in_bounds(self,i,j):

if not self._in_bounds(i,j):

return

if (i,j,False) not in self._hull_set:

heapq.heappush(self._hull_heap, self._min_tuple(i,j))

self._hull_set.add( (i,j,False) )

def _insert_max_if_in_bounds(self,i,j):

if not self._in_bounds(i,j):

return

if (i,j,True) not in self._hull_set:

heapq.heappush(self._hull_heap, self._max_tuple(i,j))

self._hull_set.add( (i,j,True) )

def __init__(self, array_a, array_b):

self._loh_a = LayerOrderedHeap(array_a)

self._loh_b = LayerOrderedHeap(array_b)

self._hull_heap = [ self._min_tuple(0,0) ]

# False for min:

self._hull_set = { (0,0,False) }

self._num_elements_popped = 0

self._layer_products_considered = []

self._full_cartesian_product_size = len(array_a) * len(array_b)

def _pop_next_layer_product(self):

result = heapq.heappop(self._hull_heap)

val, (i,j), is_max = result

self._hull_set.remove( (i,j,is_max) )

if not is_max:

# when min corner is popped, push their own max and neighboring mins

self._insert_min_if_in_bounds(i+1,j)

self._insert_min_if_in_bounds(i,j+1)

self._insert_max_if_in_bounds(i,j)

else:

# when max corner is popped, do not push

self._num_elements_popped += len(self._loh_a[i]) * len(self._loh_b[j])

self._layer_products_considered.append( (i,j) )

return result

def select(self, k):

assert( k <= self._full_cartesian_product_size )

while self._num_elements_popped < k:

self._pop_next_layer_product()

# also consider all layer products still in hull

for val, (i,j), is_max in self._hull_heap:

if is_max:

self._num_elements_popped += len(self._loh_a[i]) * len(self._loh_b[j])

self._layer_products_considered.append( (i,j) )

# generate: values in layer products

# Note: this is not always necessary, and could lead to a potentially large speedup.

candidates = [ val_a+val_b for i,j in self._layer_products_considered for val_a in self._loh_a[i] for val_b in self._loh_b[j] ]

print( 'Ratio of total popped candidates to k: {}'.format(len(candidates) / k) )

k_small_vals, large_vals = partition(candidates, k)

return k_small_vals

Listing 3. SimplifiedCartesianSumSelection.py: A simplified implementation of Listing 2. This implementation is slower when k ≪ n²; however, it has the same asymptotic runtime for any n and k: Θ(n + k).

from LayerOrderedHeap import *

class SimplifiedCartesianSumSelection:

def _min_tuple(self,i,j):

# True for min corner, False for max corner

return (self._loh_a.min(i) + self._loh_b.min(j), (i,j), False)

def _max_tuple(self,i,j):

# True for min corner, False for max corner

return (self._loh_a.max(i) + self._loh_b.max(j), (i,j), True)

def __init__(self, array_a, array_b):

self._loh_a = LayerOrderedHeap(array_a)

self._loh_b = LayerOrderedHeap(array_b)

self._full_cartesian_product_size = len(array_a) * len(array_b)

self._sorted_corners = sorted([self._min_tuple(i,j) for i in range(len(self._loh_a)) for j in range(len(self._loh_b))] + [self._max_tuple(i,j) for i in range(len(self._loh_a)) for j in range(len(self._loh_b))])

def select(self, k):

assert( k <= self._full_cartesian_product_size )

candidates = []

index_in_sorted = 0

num_elements_with_max_corner_popped = 0

while num_elements_with_max_corner_popped < k:

val, (i,j), is_max = self._sorted_corners[index_in_sorted]

new_candidates = [ v_a+v_b for v_a in self._loh_a[i] for v_b in self._loh_b[j] ]

if is_max:

num_elements_with_max_corner_popped += len(new_candidates)

else:

# Min corners will be popped before corresponding max corner;

# this gets a superset of what is needed (just as in phase 2)

candidates.extend(new_candidates)

index_in_sorted += 1

print( 'Ratio of total popped candidates to k: {}'.format(len(candidates) / k) )

k_small_vals, large_vals = partition(candidates, k)

return k_small_vals