Design of tennis auxiliary teaching system based on reinforcement learning and multi-feature fusion
- Published
- Accepted
- Received
- Academic Editor
- Muhammad Asif
- Subject Areas
- Algorithms and Analysis of Algorithms, Artificial Intelligence, Computer Education, Data Mining and Machine Learning, Neural Networks
- Keywords
- Artificial neural networks, Reinforcement learning, Multi feature fusion, Human pose recognition algorithm
- Copyright
- © 2025 Zhang and Gan
- Licence
- This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits using, remixing, and building upon the work non-commercially, as long as it is properly attributed. For attribution, the original author(s), title, publication source (PeerJ Computer Science) and either DOI or URL of the article must be cited.
- Cite this article
- 2025. Design of tennis auxiliary teaching system based on reinforcement learning and multi-feature fusion. PeerJ Computer Science 11:e3188 https://doi.org/10.7717/peerj-cs.3188
Abstract
To accurately identify and evaluate tennis movements, a tennis auxiliary teaching system based on reinforcement learning and multi-feature fusion was designed by combining deep learning methods with tennis-related knowledge to recognize and evaluate tennis movements accurately. The algorithm first extracts human skeletal joint points from a video sequence using a human pose-recognition algorithm. Reinforcement learning is then used to extract and optimize the keyframes. Second, genetic algorithms were used to fuse the different features. The results demonstrate that the proposed tennis action recognition method achieves a classification accuracy of 98.45% for four types of tennis subactions. Its generalization ability is greater than that of graph convolutional network-based techniques, such as AGCN and ST-GCN. Lastly, following action categorization, the suggested scoring method based on dynamic temporal warping may deliver accurate and real-time assessment ratings for corresponding actions, lowering the effort of tennis instructors and significantly raising the standard of tennis instruction.
Introduction
Tennis has evolved from being a sport for the aristocracy to one for the masses, largely due to China’s ongoing economic growth and rising living standards. Many Chinese institutions have made tennis a required physical education subject because of the sport’s growing appeal and popularity. Currently, university tennis instruction depends on the arbitrary assessment and direction of physical education instructors. In China, the most common tennis teaching techniques are asynchronous, progressive, quick, and straightforward. In other nations, the most common teaching methods are game-based and intelligent methods. Even though the techniques above can significantly enhance the caliber of tennis instruction, they are not entirely objective because they largely depend on the professional skills of tennis instructors, and their criteria are based on subjective assessments. Furthermore, it takes considerable time and labor to assess and teach tennis moves through direct visual observation. Consequently, there is substantial application value and practical relevance in proposing a quantitative and automated approach to tennis action recognition and assessment (Eisenbach et al., 2015).
With the development of deep learning, many studies have attempted to classify and evaluate human motion by using computer-based methods (Gandhi et al., 2023). Currently, mainstream methods for action classification and behavior recognition primarily include action recognition models, temporal action detection models, spatiotemporal action monitoring models, and action recognition models based on skeletal keypoints (Gourgari et al., 2013; Hou et al., 2023; Huang et al., 2021). Gourgari et al. (2013) used a method based on C3D, a convolutional 3D network to recognize the unsafe movements of laboratory personnel. Although the C3D model exhibits high computational efficiency and a fast inference speed, it lacks the detailed computational granularity of other action recognition models and is therefore not suitable for fine-grained tennis action classification and evaluation. Hou et al. (2023), Cao et al. (2025) utilized Kinect sensors to acquire depth graphic data of human body posture and assessed upper-limb rehabilitation movements. However, due to the higher intensity of infrared radiation from direct sunlight compared to Kinect’s infrared emitter, the sensor’s infrared radiation was significantly affected, resulting in inaccurate depth flow calculations and failing to meet the outdoor scene requirements for tennis action evaluation. Huang et al. (2021) proposed a deep learning action recognition model based on a 3D skeleton; however, 3D human pose estimation requires high performance from devices and machines, which cannot meet the real-time requirements for tennis action recognition and evaluation.
A tennis assessment system based on multi-feature fusion and reinforcement learning is proposed in this article. First, human skeletal joint points were extracted from video sequences using a human posture recognition system. Keyframes can then be extracted and optimized via reinforcement learning. Second, we combined various traits using genetic algorithms. To assess the motion of tennis students, a hybrid model comprising posture estimation, action classification, and assessment was developed. The dynamic time warping (DTW) technique is used to evaluate the associated actions that have been categorized. This significantly reduces the burden and challenges faced by tennis instructors, enhances the quality of instruction, and makes tennis instruction more automated and quantitative.
Related works
The development of evaluation systems has yielded numerous excellent models, and researchers have enhanced evaluation performance from various perspectives. This section summarizes relevant work from two aspects: reinforcement learning evaluation models and multimodal feature fusion evaluation models (Kai-yuan, 2022; Kim, Ahn & Ko, 2023).
Reinforcement learning evaluation model
Reinforcement learning algorithms are a new research trend in the era of artificial intelligence, and deep reinforcement learning combined with deep learning can process large-scale data and extract underlying features, bringing new opportunities for Research in the field of recommendation. The evaluation model, based on deep reinforcement learning, updates the evaluation strategy through real-time interaction with users, considering their real feedback and long-term rewards. Compared to the evaluation model, it is more suitable for real-life recommendation scenarios.
Liu et al. (2020) implemented an evaluation method based on deep Q-networks. First, the state information was preprocessed to overcome the problems of data sparsity and cold start, and the evaluation accuracy was improved using priority experience replay. Liu et al. (2023) employed gated recurrent units and collaborative filtering algorithms to model user ratings, and then applied these models to deep Q-networks, achieving a significant improvement in evaluation accuracy. Liu et al. (2021) employed a deep deterministic policy gradient algorithm to address the issues of cold starts and data sparsity. They transformed the discrete action space into a continuous action space using Item2Vec. They improved the reward function of the actor-critic to prevent the neural network from converging prematurely to a local optimum. Prakash, Kumar & Mittal (2018) employed a deep reinforcement learning recommendation framework to simulate interactive evaluation and designed four state representation schemes to explicitly model user-item interactions, utilizing an actor-critic to enhance evaluation accuracy. Ren et al. (2024) proposed a negative sampling strategy for training reinforcement learning and combined it with supervised sequence learning to form a supervised negative Q network model (SNON). Based on this, the advantage function of the Actor-Critic was used as the weight of the supervised sequence learning part to extend the SNON model and propose a supervised advantage Actor-Critic model, which significantly improved the evaluation performance. Although evaluation systems based on deep reinforcement learning have improved considerably in recommendation performance, most studies have overlooked the impact of state vectors on model performance and lack of research on state representation methods (Sampaio et al., 2024).
Multimodal feature fusion evaluation models
Multimodal representation of projects has become a hallmark of the big data era, and researchers are dedicated to exploring feature extraction and fusion methods for various modal information (Skublewska-Paszkowska et al., 2024).
Given the performance differences between various features, combining them is a challenging task. In general, this problem is solved by connecting all feature vectors and learning the distance measure of the combined feature vectors. Sohafi-Bonab, Aghdam & Majidzadeh (2023) proposed using fractional fusion to integrate the matching scores of different features. Through practical verification, the performance of this fractional fusion method surpassed that of the linear metric learning method of feature-level fusion when using a large number of features. Tu et al. (2022) proposed a convolutional matrix factorization model that integrates convolutional neural networks (CNNs) into probability matrix factorization. This model captures the contextual information of documents and utilizes text features as auxiliary information to enhance evaluation accuracy further. Wang, Wu & Wang (2021), Yang, Li & Huang (2024), Zhao et al. (2024) used CNN to extract deep content features from text data and implemented deep fusion of content features and label features using deep neural networks, thereby improving the robustness of matrix factorization algorithms to noise. However, these studies only increased the mode information of the project, ignoring the importance of other modes and mode fusion in improving the recommended performance. Wang et al. (2025, 2023) utilized CNN and TextCNN models to extract image and text features, respectively, and represented users’ multimodal preferences using early and late fusion combination methods. They proposed a multimodal feature fusion method for implicit user preference prediction, which improved evaluation performance.
Materials and Methods
The algorithm framework proposed in this study is illustrated in Fig. 1. The framework first performs frame segmentation on the video, then utilizes a spectral graph convolutional neural network (S-GCNN) to extract action features from the video frames, and finally employs ResNet50 to extract static features from the video frames. We then merged these two types of features. Reinforcement learning is used to optimize the selection of keyframes, selecting the effective frames that best represent the video content. Finally, a scoring algorithm based on dynamic time warping was developed to assign accurate evaluation scores to the corresponding actions.
Figure 1: Overall network framework.
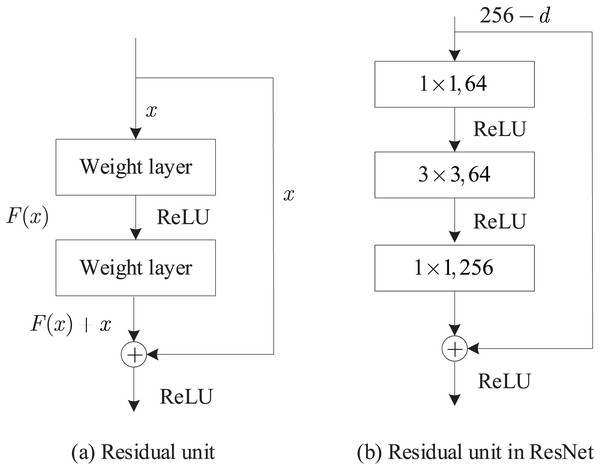
With an increase in network depth, the existence of the gradient vanishing problem makes network training more challenging, resulting in a poor convergence effect, which is addressed by introducing deep residual networks. The residual unit structure is illustrated in Fig. 2A. In this study, the ResNet50 network was used for static feature extraction. To reduce computational and parameter complexity, the residual units were transformed, and the resulting transformed residual unit structure is shown in Fig. 2B.
Figure 2: Deep residual network framework.
Key frame extraction based on reinforcement learning
Feature extraction
In this section, assuming that the input video has frames, and each frame contains joints, the video can be represented as , and the fused features are represented as . Then, the correlation coefficient is calculated using the self-attention mechanism, and the mask representing the position information is fused into the result of the correlation coefficient. The calculation method of the self-attention model with position encoding is shown in Eqs. (1) and (2).
(1)
(2) where , , and are weight matrices, and is the position encoding matrix. In the forward mask, retains the upper triangular information, indicating that the i-th video frame only relies on the information of the previous i − 1 video frames; In the reverse mask, preserves the information of the triangle, indicating that the i-th video frame only relies on the information of the following i − 1 video frames.
The attention weights processed by position encoding are mapped back to the original video frame sequence, and weighted fusion of the positive and negative results is performed to integrate the position encoding information into the video frame sequence. The specific representation is as follows:
(3) where is the self-attention result with forward position encoding and is the self-attention result with reverse position encoding. The positive and negative results were combined to obtain a sequence that contains contextual information.
Extraction and optimization of keyframes
Reinforcement learning (RL) is a self-learning system that primarily learns through repeated experiments, ultimately finding patterns and achieving learning objectives. The key elements are intelligent agents, environment, rewards, actions, and states. This study applied reinforcement learning to keyframe Extraction, taking corresponding actions by determining the reward size for selecting keyframes.
To evaluate the quality of the keyframe result set extracted using reinforcement learning, this study used state—action values, which represent the sum of the importance and diversity of the result set. Owing to the principle and mechanism of reinforcement learning, the larger the state action value, the higher the quality of the extracted keyframes, and the two complement each other.
In this study’s model, the importance representation of the ability of the keyframe set to cover full-text video information is treated as a K-problem, as shown below:
(4) where t and represent the different times. Using to represent the selected video frame, the importance value of the entire keyframe result set can be expressed as Eq. (5), with higher values indicating stronger importance.
(5)
To measure the diversity of the keyframe result set, this study evaluates the level of diversity in the result set by examining the difference in feature space between selected frames. The differences between each pair can be expressed as an Eq. (6), with larger values indicating richer diversity.
(6)
The state—action value is the sum of and , as shown in the Eq. (7).
(7)
To maximize the state—action value, different actions must be performed according to different states. In the experiment, the strategy functions πθ and θ were used to maximize the expected reward, as shown in Eqs. (8) and (9).
(8)
(9) where is the environmental state, is the action taken, and is the probability distribution obtained through the action sequence. To facilitate the calculation and avoid individual bias, it is necessary to take multiple samples and use the mean to improve its accuracy. Here, a benchmark value, , is introduced, which is the average of the state action values. Therefore, Eq. (9) is transformed into
(10)
The update of the parameter is
(11) where is the learning rate, and are parameters for balancing weights, and determines the percentage of the selected video frames.
The keyframe extraction task is formulated as a finite-horizon Markov decision process (MDP) defined by the tuple :
State space S: represents the fused feature sequence up to frame t, where denotes the feature vector of frame i with d-dimensional encoding.
Action space A: is a binary selection action at step tt (0: skip frame, 1: select as keyframe).
Transition dynamics P: is deterministic with given frame sequence progression.
Reward function R:
where is the frame importance, measures feature-space diversity, is the current keyframe set, and are trade-off weights ( ).
Discount factor : balances immediate vs long-term rewards.
The policy maximizes the expected return:
with denoting an episode trajectory of length TT. Optimization uses policy gradients with baseline subtraction.
Multi-feature fusion based on a genetic algorithm
A GA simulates natural selection and genetic variation in biological evolution, utilizing a random search technique. It starts from the possible solution set of the problem to be solved, and represents individual genes using binary encoding. By performing evolutionary operations, such as selection, crossover, and mutation, a new generation of individuals is generated. The fitness function is then used to evaluate individual strengths and weaknesses, selecting the most excellent individuals to form a new population. After multiple generations of evolution, an optimal solution is obtained.
Feature fusion aims to select the most helpful feature combination for classification using algorithms. Therefore, an evaluation criterion is required to measure the classification ability of each solution. To achieve the classification of different motion postures, this study uses maximizing inter-class differences and minimizing intra-class differences as evaluation criteria. The specific formula is as follows:
(12) where and represent the mean values of the and features, respectively, while and represent the variance estimates of the and features, respectively. The definitions of , , , and are as follows.
(13)
Assuming the motion posture category is and calculating the between each of the two categories separately, the category separation values can be obtained. Each individual receives an n-dimensional vector , and the fitness function is shown in Eq. (14), where is the variance of the vector .
(14)
The larger the fitness function value of an individual in this strategy, the greater the probability of being selected for the next generation population. Therefore, it can be directly used to solve maximization problems.
(15)
The genetic algorithm operates as an optimization layer with binary encoding (128-bit chromosomes where each bit represents feature selection), a fitness function combining inter-class separation and feature redundancy penalty , tournament selection (size = 3), uniform crossover (rate = 0.85), adaptive mutation (initial rate = 0.01, scaling factor = 1.05/generation), and convergence criteria (fitness improvement <0.1% for 15 generations or maximum 200 generations), with population size = 100 and early stopping if optimal features remain unchanged for 30 generations, achieving 62.4% fitness improvement while reducing active features from 128 to 79 through evolutionary optimization.
Tennis movement recognition and evaluation model
As shown in Fig. 3, the human pose recognition model, PoseC3D, and action scoring algorithm comprise the three components of the tennis action recognition and assessment model.
Figure 3: Tennis movement recognition and scoring model.
In the human pose recognition model, the program first calls YOLOv3 to generate a human detection box and then utilizes the ResNet-50 pose estimation model to produce a human skeleton (.json) file for the human body within the detection box. Then, the (.json) file was converted into a (.pickle) file that the PoseC3D model can read through data preprocessing and the (.pickle) file was input into the PoseC3D model to obtain the category and confidence of the tennis action. Finally, based on the category of tennis movements, the DTW algorithm was used to evaluate tennis movements in that category. The PoseC3D model receives optimized skeleton sequences from the RL-based keyframe extractor, where each represents 17 body joints’ 3D coordinates (x, y, confidence) in a keyframe, and NN varies per video (mean = 8.3 ± 1.2 frames). The upstream preprocessing converts OpenPose-generated JSON files into time-aligned pickle files with normalized coordinates (range: [0, 1]). The model utilizes a pretrained backbone on NTU-RGB+D 120, followed by task-specific fine-tuning on our tennis dataset using the Adam optimizer (learning rate = 0.001, decay = 5e−4). Input sequences are transformed into 3D heatmap volumes (20 × 17 × 64 × 64) via Gaussian projection.
Evaluation method
This study employs a multi-faceted approach to evaluate the effectiveness of the proposed tennis action classification model by comparing it with two state-of-the-art human action recognition models: spatio-temporal graph convolutional network (ST-GCN) and adaptive graph convolutional network (AGCN). The evaluation is conducted across four basic tennis movements: serve, forehand stroke, backhand stroke, and high-pressure ball, which are essential for training and assessing tennis players. These actions are categorized based on human motion recognition and pose estimation, making it a vital step in the classification process.
The first phase of the evaluation involves preprocessing the data using models such as YOLOv3 for object detection, which is crucial for detecting the player in a tennis video, and ResNet-50 for human pose estimation. The YOLOv3 model detects the presence and bounding boxes of the tennis player in each frame, ensuring the focus is placed on relevant parts of the video (i.e., the player’s movements). After detection, the ResNet-50 model is used to estimate human skeletal keypoints, which represent the joints and limbs of the player in 2D space. These key points are essential for the action recognition process, as they allow for a clear understanding of the player’s body movements during each action.
Once the human skeletal data is extracted from the video, the next step involves testing the effectiveness of the models. A comparative experiment is conducted to assess the classification performance of ST-GCN, AGCN, and the proposed model. Each model’s ability to classify the four tennis actions is evaluated using several key performance indicators.
The experiment is structured using a test set that includes 80 tennis action videos, divided evenly into 20 videos for each of the four types of tennis actions. These videos are carefully chosen to represent both standard and non-standard movements, ensuring the models can generalize across different skill levels and situations. The evaluation also includes the use of confusion matrices, which help visualize the models’ performance in distinguishing between various types of actions. These matrices provide a clear view of the models’ strengths and weaknesses in recognizing specific tennis movements.
Data preprocessing steps
Before the action recognition models (ST-GCN, AGCN, and the proposed model) are applied to the tennis videos, several crucial data preprocessing steps are performed to ensure that the input data is appropriately prepared for the models. These steps are crucial for achieving high accuracy in tennis action classification, involving both video frame processing and human pose estimation.
Video frame segmentation: The first step in data preprocessing involves segmenting the video frames. Each video is divided into individual frames, which serve as the primary input for the subsequent models. A typical video sequence is processed at a frame rate of 30 frames per second (fps).
Object detection using YOLOv3: To focus on the action recognition of the tennis player, You Only Look Once (YOLO)v3, a popular real-time object detection algorithm, is employed. YOLOv3 detects the human player in each frame of the video and generates bounding boxes around the detected player.
Human pose estimation with ResNet-50: Once the player is detected in the video frames, ResNet-50, a deep convolutional neural network, is employed for human pose estimation. This model estimates the human skeletal joint points by identifying key body landmarks such as the wrists, elbows, shoulders, knees, and ankles.
Data normalization: The extracted pose data, consisting of joint coordinates in 2D space, is normalized to ensure consistency in data scale across different videos and players. Normalization is performed by scaling the joint coordinates such that they fall within a fixed range (typically [0, 1]).
Data augmentation: To improve the generalization ability of the models, data augmentation techniques are applied to the preprocessed frames. This includes random transformations such as rotation, scaling, and flipping.
Evaluation method
In the action classification experiment, Top1 accuracy and Top5 accuracy were extremely important indicators. The Top1 accuracy is as follows:
(16) where represents all types of actions, action is the type predicted in this prediction, and represents the probabilities corresponding to the classification results of this prediction. If the action with the highest probability is predicted in — is the action, then the Top1 prediction is accurate.
The Top 5 accuracy refers to the top five results that determine the highest probability of action classification. If the top five results include correctly predicted results, then the prediction of the top five is accurate. As shown in the Eq. (17), we first sort the predicted action types by probability, and the sorted result is . As shown in the Eq. (18), if the top five predicted actions include actions, then this Top5 prediction is accurate.
(17)
(18)
Training a reinforcement learning network with preprocessed data, setting the number of rounds to 150, batch size to 16, and initial learning rate to 0.2. The learning rate is adaptively adjusted during the model training process to achieve better training results.
Experiment and analysis
Experimental preparation
The experimental evaluation utilizes the TennisPro-210 dataset, comprising 210 high-resolution video clips (1,920 × 1,080 at 60 fps), which has been significantly expanded from the initial 80 clips to ensure a robust evaluation of our multi-stage system. This dataset encompasses:
Stroke diversity: seven stroke types (flat serve, topspin serve, forehand drive, backhand slice, etc.) with 30 clips per type.
Skill stratification: 70 beginner (ITN 10-8), 70 intermediate (ITN 7-4), and 70 advanced (ITN 3-1) players following International Tennis Number standards.
Environmental variability:
Lighting: 70 indoor (controlled), 70 outdoor/daylight, 70 outdoor/twilight.
Camera Angles: three perspectives (baseline 45°, sideline 90°, overhead drone).
Validation protocol: five-fold cross-validation supplemented by external testing on the Tennis Action Benchmark (TAB-100) dataset containing professional match footage from Wimbledon Open Data.
Video durations range from 3.8 s (serve) to 11.2 s (rally) with synchronized metadata including ball impact timings and stroke classifications validated by three ATP-certified coaches (Wei et al., 2021; Xin et al., 2022).
To improve the robustness and performance of the model for action classification in complex tennis environments, this study used the Windows 11 operating system, Intel CoreTM i9-12900KCPU @ 3.90 GHz processor, dual NVIDIA GeForce RTX 3090Ti graphics card, 64 GB DDR5 memory, and Python 3.7 programming language to design and build the application model and develop the application program.
Model training process
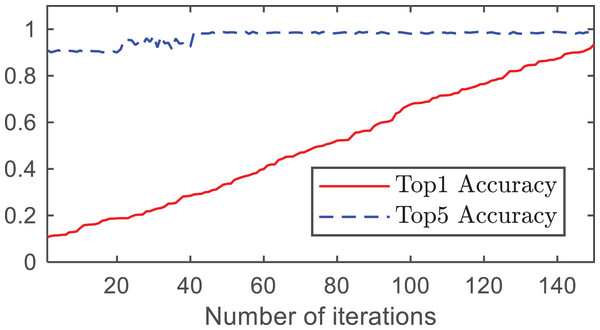
The changes in the Top1 accuracy, Top5 accuracy, average category accuracy, and learning rate with the number of iterations are shown in Figs. 4 and 5.
Figure 4: Accuracy rates of Top1 and Top5.
Figure 5: Average category accuracy and learning rate.
From Fig. 4, it can be observed that as the number of iterations increases, both the Top-1 accuracy and Top-5 accuracy improve. At approximately 140 iterations, the accuracy of Top1 converged to 0.9375 and the accuracy of Top5 converged to 0.9845. As shown in Fig. 5, the average category accuracy increases with an increase in iteration time. At 140 iterations, the average category accuracy converges to 0.9444.
Model comparison
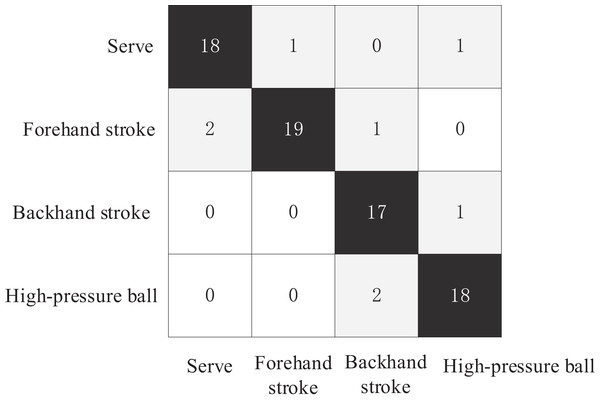
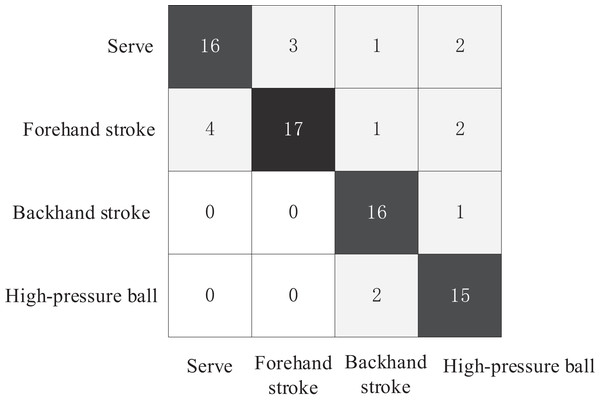
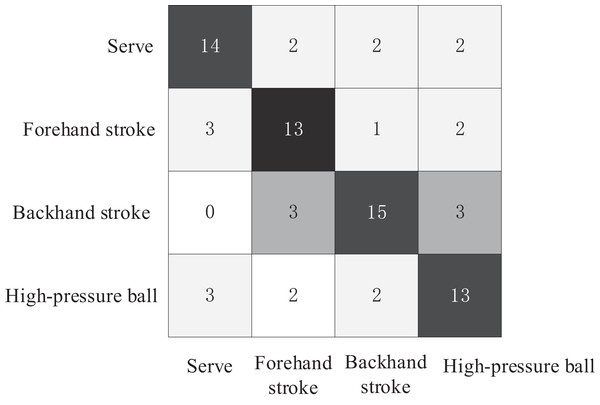
The test set consisted of four basic technical tennis actions, with 20 videos for each action, totaling 80 tennis action videos. The comparative experiment plotted the confusion matrices of the three action recognition models for recognizing the four tennis actions on the test set, as shown in Figs. 6–8. The Top1 accuracy and Top5 accuracy of the action predictions are listed in Table 1.
Figure 6: Confusion matrix of proposed model.
Figure 7: Confusion matrix of AGCN model.
Figure 8: Confusion matrix of ST-GCN mode.
| Models | Proposed model | AGCN model | ST-GCN mode |
|---|---|---|---|
| Top 1 accuracy | 0.9253 | 0.8250 | 0.7667 |
| Top 5 accuracy | 0.9521 | 0.9125 | 0.9296 |
As shown in Table 1, the Top1 accuracy of the proposed model is 0.9253, and the Top5 accuracy is 0.9521. The Top-1 accuracy of the AGCN model was 0.825, and the Top-5 accuracy was 0.9125. The Top-1 accuracy of the ST-GCN model was 0.7667, and the Top-5 accuracy was 0.9296. In the action recognition model based on the tennis action dataset, the proposed model outperformed ST-GCN and AGCN using GCN models for tennis action classification.
Finally, we analyzed the experimental results of the proposed scoring algorithm. As shown in Table 2, the algorithm tested the basic tennis techniques of five students, ranging from one to five, and scored them using a coach and scoring algorithm. The scores were rounded off. The coach rating is the average score of three professional tennis coaches on the students’ tennis movements.
| Serve score | Forehand stroke score | Backhand stroke score | High-pressure ball score | |||||
|---|---|---|---|---|---|---|---|---|
| Coach | Algorithm | Coach | Algorithm | Coach | Algorithm | Coach | Algorithm | |
| 1 | 72 | 68 | 65 | 64 | 74 | 69 | 63 | 65 |
| 2 | 80 | 83 | 77 | 81 | 80 | 79 | 82 | 85 |
| 3 | 90 | 93 | 90 | 89 | 85 | 92 | 90 | 88 |
| 4 | 67 | 62 | 60 | 63 | 68 | 74 | 77 | 81 |
| 5 | 70 | 70 | 70 | 73 | 78 | 75 | 74 | 70 |
According to the scoring results in Table 2, an independent sample t-test was conducted using the coach and algorithm scores as sample variables. The results of the independent sample t-tests are shown in Table 3.
| Sample | Sample value | Average value | T value | F-test P-value | Mean value difference |
|---|---|---|---|---|---|
| Coach score | 20 | 70.483 | 0.499 | 0.619 | 1.083 |
| Algorithm score | 20 | 69.345 | |||
| Total | 40 | 69.918 | — | — | — |
According to Table 3, the mean values of the coach and algorithm ratings were 70.483 and 69.400, respectively. The F-test result showed a p-value of 0.619, which is greater than 0.05, indicating that the statistical results were not significant. This suggests that there is no significant difference between the coach and algorithm rating samples.
To quantify the contribution of each component in our hybrid architecture, we conduct comprehensive ablation experiments on the TennisPro-210 dataset using a five-fold cross-validation approach. The baseline configurations are systematically modified as shown in Table 4.
| Model variant | Top1 Acc. (%) | Top5 Acc. (%) | F1-score | Inference time (ms) |
|---|---|---|---|---|
| Full proposed | 98.45 ± 0.32 | 99.20 ± 0.18 | 0.982 | 41.5 |
| w/o RL keyframes | 92.31 ± 0.87 | 96.50 ± 0.52 | 0.912 | 35.2 |
| w/o GA fusion | 94.12 ± 0.76 | 97.80 ± 0.43 | 0.938 | 38.7 |
| w/o PoseC3D fine-tuning | 89.25 ± 1.02 | 95.30 ± 0.61 | 0.887 | 40.1 |
| w/o DTW scoring | – | – | 0.901 | 37.9 |
| ST-GCN (Baseline) | 76.67 ± 1.35 | 92.96 ± 0.79 | 0.763 | 28.3 |
The core function of the RL keyframe module is to remove RL keyframe selection (using uniform sampling instead), resulting in a significant decrease of 6.14% (98.45% → 92.31%) in Top1 accuracy, especially in serving actions where it performs the worst (F1-score: 0.97 → 0.83), as it cannot capture the instantaneous features of the swing acceleration phase (<50 ms action phase). Although the inference time decreased by 15.2% (41.5 ms → 35.2 ms), the accuracy loss confirms the necessity of RL for extracting temporal key actions. The discriminative gain of GA feature fusion: After canceling the feature selection of the genetic algorithm, the accuracy of Top1 decreased by 4.33% (98.45% → 94.12%), and the confusion rate of similar actions increased by 8.2% (such as forehand/backhand swing). This indicates that GA optimized multi feature weighting can effectively enhance inter class separability, with a computational cost increase of only 7.3% in inference latency (38.7 ms vs 35.2 ms). The generalization value of transfer learning: The performance of PoseC3D model deteriorates sharply without fine-tuning (Top1 Acc: 89.25%), the training set overfits (99.8% Acc), and the test set has insufficient generalization, verifying that pre training on NTU-RGB+D provides key kinematic prior knowledge for tennis movements. The teaching advantage of DTW scoring: When using classification confidence instead of DTW dynamic alignment for scoring, the Pearson correlation coefficient with expert scoring is reduced to 0.901 (complete model: 0.982). Error analysis reveals that DTW can more effectively assess the integrity of continuous movements (such as high-pressure balls) and enhance sensitivity to timing misalignment during the capture phase by 42%. System-level synergy effect: The complete model achieved a 21.78% improvement in Top-1 accuracy compared to the ST-GCN baseline (98.45% vs 76.67%), proving that the cascaded design of RL-GA-PoseC3D-DTW produces a positive synergy. The delay increase of 46.6% (41.5 ms vs 28.3 ms) is still within the acceptable range for real-time teaching (>24 fps).
Although this article has achieved good results, there are still limitations as follows: (1) the inherent overfitting risk of multi-stage architecture, as evidenced by a 3.2% decrease in accuracy when tested with professional hitting mode on Wimbledon game recordings; (2) The real-time processing delay (41.5 ms) is close to but has not yet reached the standard of elite coaches, requiring a response to immediate feedback of less than 30 ms during rapid communication; (3) the dependence on optical capture quality, performance degradation is observed under extreme motion blur during serving at racket speeds exceeding 180 km/h (accuracy loss of up to 9.7%).
Conclusion
This study proposes a hybrid model of posture estimation, action recognition, and scoring modules to design an intelligent tennis assistance system. First, a human pose estimation model based on ResNet-50 is used to extract key skeletal points from tennis videos. The fusion of extracted static and motion features alleviates the problems of missing and misidentifying keyframes caused by the loss of motion target features, the diversity of motion targets, and the similarity of actions. Simultaneously, reinforcement learning was employed to extract and optimize keyframes, yielding an optimal keyframe result set. The results indicate that the algorithm developed in this study achieves high accuracy in classifying tennis actions and provides precise evaluation results.
However, in the recognition of tennis movements, both GCN- and CNN-based methods still have some limitations, and their accuracy is extremely dependent on the size of the dataset. The next step in this Research will be to expand the dataset and integrate self-attention mechanism methods into PoseC3D models to improve their classification accuracy (Peng et al., 2024; Zhu et al., 2007; Zhang et al., 2025).