A filter design for T-S fuzzy systems based on moving horizon estimator with measurement noise

Plant form

We think about a nonlinear device represented by way of a discrete-time T-S fuzzy model, as follows: Rule i: IF θ_1,m is M_i1 and ... and θ_p,m is M_ip, then (1)${\displaystyle \left\{\begin{array}{c}{x}_{m+1}=A_i{x}_m+B_{2i}{u}_m+B_{1i}{\omega }_m\hfill \\ z_m=C_i{x}_m+D_{2i}{u}_m+{\omega }_m\hfill \\ x_m={\psi }_m\hfill \\ \hfill \end{array}\right.}$ where in the premise rules, i = 1,2,…,r, θ_m = [θ_1,m, θ_2,m, …, θ_p,m] is the premise variables vector, M = [M_i1, M_i2, …, M_ip] is the fuzzy set, x_m ∈ ℝ^a is the state vector, z_m ∈ ℝ^b is the measured output, u_m ∈ ℝ^c is the input signal, ω_m ∈ ℝ^l represents the disturbance input vector, which is considered to be part of l₂[0, ∞), and r is the number of IF-THEN rules. A_i, B_1i, B_2i, C_i, D_2i are known matrices with the appropriate dimensions.

The fuzzy basis functions are defined as follows: (2)${\displaystyle h_i\left({\theta }_m\right)=\frac{\prod _{j=1}^p{M}_{ij}\left({\theta }_{j,m}\right)}{\sum _{i=1}^r{\Pi }_{j=1}^p{M}_{ij}\left({\theta }_{j,m}\right)}}$ where, for all m values, we have ${\prod }_{j=1}^p{M}_{ij}\left({\theta }_{j,m}\right)\ge 0$ (i = 1, 2, …, r), and ${\sum }_{i=1}^r{\prod }_{j=1}^p{M}_{ij}\left({\theta }_{j,m}\right)>0$. Therefore, for all m values the fuzzy basis functions satisfy the equations h_i(θ_m)⩾0 (i = 1, 2, …, r) and ${\sum }_{i=1}^r{h}_i\left({\theta }_m\right)=1$.

Combine the fuzzy basis function with the proposed nonlinear system to get the following formula, which can be used for discrete systems under T-S fuzzy modeling: (3)${\displaystyle \left\{\begin{array}{ccc}{x}_{m+1}\hfill & =\sum _{i=1}^r{h}_i\left({\theta }_m\right)\left(A_i{x}_m+B_{2i}{u}_m+B_{1i}{\omega }_m\right)\hfill & \hfill \\ z_m\hfill & =\sum _{i=1}^r{h}_i\left({\theta }_m\right)\left(C_i{x}_k+D_{2i}{u}_m+{\omega }_m\right)\hfill \\ x_m\hfill & ={\psi }_m\hfill \\ \hfill \end{array}\right.}$ For the convenience of calculation, we refer to experience to set the controller as a function related to the state feedback (Dong, Wang & Gao, 2009), that is, u = kx. Then Eq. (3) can be replaced by (4)${\displaystyle \left\{\begin{array}{ccc}{x}_{m+1}\hfill & =\sum _{i=1}^r{h}_i\left({\theta }_m\right)\left({\widehat{A}}_i{x}_m+B_{1i}{\omega }_m\right)\hfill & \hfill \\ z_m\hfill & =\sum _{i=1}^r{h}_i\left({\theta }_m\right)\left({\widehat{C}}_i{x}_m+{\omega }_m\right)\hfill \\ x_m\hfill & ={\psi }_m\hfill \\ \hfill \end{array}\right.}$ where ${\widehat{A}}_i=A_i+k{B}_{2i}$, ${\widehat{C}}_i=C_i+k{D}_{2i}$. The MHE process for the T-S fuzzy system is still difficult to develop using this approach, so we further define ${\displaystyle \begin{array}{ccc}{\overline{A}}_m\hfill & =\sum _{i=1}^r{h}_i\left({\theta }_m\right){\widehat{A}}_i,\hfill & {\overline{B}}_m=\sum _{i=1}^r{h}_i\left({\theta }_m\right)B_{1i}\hfill \\ {\overline{C}}_m\hfill & =\sum _{i=1}^r{h}_i\left({\theta }_m\right){\widehat{C}}_i,\hfill & {\overline{D}}_m=\sum _{i=1}^r{h}_i\left({\theta }_m\right)\hfill & \hfill \\ \hfill \end{array}}$ Here, we design the filters of a general structure by (5)${\displaystyle \left\{\begin{array}{ccc}{x}_{m+1}\hfill & ={\overline{A}}_m{x}_m+{\overline{B}}_m{\omega }_m\hfill & \hfill \\ z_m\hfill & ={\overline{C}}_m{x}_m+{\overline{D}}_m{\omega }_m\hfill \\ x_m\hfill & ={\psi }_m\hfill \\ \hfill \end{array}\right.}$ The above formulas provide a great basis for our subsequent derivation.

MHE for the T-S fuzzy model

Using the known information during this period of time such as z_m−L, z_m−L+1, …, z_m and u_m−L, u_m−L+1, …, u_m with the integer L ≥ 1, we get the estimate through the MHE at time m. Using Eq. (5), we get the following formula between x_m+1 and z_m: (6)${\displaystyle x_{m+1}=\left({\overline{A}}_m-{\overline{B}}_m{\overline{D}}_m^{-1}{\overline{C}}_m\right)x_m+{\overline{B}}_m{\overline{D}}_m^{-1}{z}_m}$ For brevity, the following formula is used: (7)${\displaystyle x_{m+1}={\Phi }_m{x}_m+{\Omega }_m{z}_m}$ where ${\Phi }_m={\overline{A}}_m-{\overline{B}}_m{\overline{D}}_m^{-1}{\overline{C}}_m$, ${\Omega }_m={\overline{B}}_m{\overline{D}}_m^{-1}$. Using Eqs. (5) and (7), L + 1 equations are iterated as shown below: (8)${\displaystyle \begin{array}{ccc}{z}_{m-L}\hfill & ={\overline{C}}_{m-L}{x}_{m-L}+{\overline{D}}_{m-L}{\omega }_{m-L}\hfill & \hfill \\ z_{m-L+1}\hfill & ={\overline{C}}_{m-L+1}{\Phi }_{m-L}{x}_{m-L}+{\overline{C}}_{m-L+1}{\Omega }_{m-L}{z}_{m-L}+{\overline{D}}_{m-L+1}{\omega }_{m-L+1}\hfill \\ z_{m-L+2}\hfill & ={\overline{C}}_{m-L+2}{\Phi }_{m-L+1}{\Phi }_{m-L}{x}_{m-L}+{\overline{C}}_{m-L+2}{\Phi }_{m-L+1}{\Omega }_{m-L}{z}_{m-L}\hfill \\ \hfill & +{\overline{C}}_{m-L+2}{\Omega }_{m-L+1}{z}_{m-L+1}+{\overline{D}}_{m-L+2}{\omega }_{m-L+2}\hfill \\ \hfill & ⋮\hfill \\ z_m\hfill & ={\overline{C}}_m\prod _{i=1}^L{\Phi }_{m-i}{x}_{m-L}+{\overline{C}}_m\sum _{j=1}^{L-1}\prod _{i=1}^j{\Phi }_{m-i}{\Omega }_{m-j-1}{z}_{m-j-1}+{\overline{C}}_m{\Omega }_{m-1}{z}_{m-1}+{\overline{D}}_m{\omega }_m\hfill \\ \hfill \end{array}}$

From Eq. (8) we know that the evaluate of measured output at the present time m can be solved by the measured outputs at the time m − 1, m − 2, m − 3, …, m − L, the state of the system at the time m − L and the measurement noise at the current time m.

Remark 1: Here, we define ${\overline{D}}_m$ is an expression about fuzzy basis function in ${\overline{D}}_m={\sum }_{i=1}^r{h}_i\left({\theta }_m\right)$, without the coefficient matrix in the state space expression. Obviously, ${\overline{D}}_m$ here is an invertible matrix of dimension one.

Remark 2: Kalman filter algorithm is based on accurate mathematical model and is sensitive to error. So the MHE in the T-S fuzzy system is proposed, which uses a fixed number of measurements for estimation. In this article, we derive a series of iterative formulas in order to obtain the relationship between x_m−L and z_m−L, z_m−L+1, …, z_m within the fixed-length estimation window set by MHE.

Input-to-state stability (ISS)

Non-linear systems with external disturbances are considered as follows: (15)${\displaystyle x_{m+1}={\overline{A}}_m{x}_m+{\overline{B}}_m{\omega }_m.}$ Here, we provide two ISS definitions.

Lemma 1  Alessandri, Baglietto & Battistelli (2008) The system in Eq. (15) is input-to-state stable (ISS) if there exist the function β ∈ KL and the function γ ∈ K_∞ such that for each external input ω(m) and each initial condition $x_0={\overline{x}}_{m-L}$, solutions exist and satisfy (16)${\displaystyle \parallel x_{m,x_0,{\omega }_m}\parallel \le \beta \left(\parallel x_0,L\parallel \right)\le \gamma \left({\omega }_m\right)}$ where ∥x_m,x0,ωm ∥ is the solution to the system in Eq. (15) at time m.

Lemma 2  Kim et al. (2006) The system in Eq. (15) is input-to-state stable (ISS) if and only there exists the continuous ISS-Lyapunov function V: Rⁿ → R ≥ 0 such that for the functions λ₁, λ₂, λ₃, σ ∈ K_∞, the Lyapunov function V satisfies (17)${\displaystyle {\lambda }_1\parallel x_m\parallel \le V\left(x_m\right)\le {\lambda }_2\parallel x_m\parallel }$ and (18)${\displaystyle V\left(x_{m+1}\right)-V\left(x_m\right)\le -{\lambda }_3\parallel x_m\parallel +\sigma \parallel {\omega }_m\parallel }$ or (19)${\displaystyle V\left(x_{m+1}\right)-V\left(x_m\right)\le -{\lambda }_3\parallel x_{m+1}\parallel +\sigma \parallel {\omega }_m\parallel }$

ISS of the proposed MHE

Before proving ISS of the system in Eq. (15) under the MHE, we need to calculate the estimation of x_m−L considering the cost function J at time m having the smallest value, such that the cost function J satisfies (20)${\displaystyle \frac{\partial J}{\partial {\hat{x}}_{m-L|m}}=0}$ By calculation, we obtain the equation for ${\hat{x}}_{m-L\left|m\right|}$ as follows: (21)${\displaystyle 2{\Sigma }_{m-L}^{-1}\left({\hat{x}}_{m-L|m}-{\overline{x}}_{m-L}\right)=0}$ Using Eq. (21), the solution can be obtained by (22)${\displaystyle {\hat{x}}_{m-L|m}={\overline{x}}_{m-L}.}$ This subsection introduces the stability characteristics of the estimation error of the proposed unconstrained estimator. Using Eq. (22), the estimated error e_m−L is given as follows: (23)${\displaystyle \begin{array}{ccc}{e}_{m-L}=\hfill & x_{m-L}-{\hat{x}}_{m-L|m}\hfill & \hfill \\ \hfill & =x_{m-L}-{\overline{x}}_{m-L}\hfill \\ \hfill & ={\Phi }_{m-L-1}{x}_{m-L-1}+{\Omega }_{m-L-1}{z}_{m-L-1}-{\Phi }_{m-L-1}{\hat{x}}_{m-L-1|m-L-1}-{\Omega }_{m-L-1}{z}_{m-L-1}\hfill \\ \hfill \end{array}}$ Then, we get the estimated error dynamics: (24)${\displaystyle e_{m-L}={\Phi }_{m-L-1}{e}_{m-L-1}.}$ The pair $\left({\overline{C}}_m,{\overline{A}}_m\right)$ is completely observable in L step.

Theorem : Consider a pair {${\overline{x}}_{m-L}$ and Z_m,L} and suppose that Assumption 1 holds. If there exists a scaler μ and symmetric matrices P₁ > 0, P₂ > 0 satisfy (25)${\displaystyle \parallel {\Phi }_{m-L-1}\parallel <1}$ (26)${\displaystyle P_2-P_1\le -Q_1}$ (27)${\displaystyle P_2-P_1\ge -Q_2}$ for some Q₁ > 0, Q₂ > 0, then the estimation error dynamics e_m−L are ISS.

Proof: If ∥Φ_m−L−1 ∥  < 1, then ρ(Φ_m−L−1) < 1 is obtained, that means that there is always a matrix P₁ that satisfies (28)${\displaystyle {\Phi }_{m-L-1}^T{P}_1{\Phi }_{m-L-1}-P_1\le -Q_1}$ for any $Q_1=Q_1^T>0$. Simple algebraic manipulations show that (29)${\displaystyle \parallel {\Phi }_{m-L-1}{e}_{m-L-1}{\parallel }_{P_1}^2-\parallel e_{m-L-1}{\parallel }_{P_1}^2\le -\parallel e_{m-L-1}{\parallel }_{Q_1}^2}$ Using Eq. (24), the following equality can be obtained: (30)${\displaystyle \parallel {\Phi }_{m-L-1}{e}_{m-L-1}{\parallel }_{P_1}^2-\parallel e_{m-L-1}{\parallel }_{P_1}^2=\parallel e_{m-L}{\parallel }_{P_1}^2}$ Combining Eqs. (29) and (30) yields (31)${\displaystyle \parallel e_{m-L}{\parallel }_{P_1}^2\le \parallel e_{m-L-1}{\parallel }_{Q_1-P_1}^2}$ Consider the Lyapunov candidate V: $V\left(e_{m-L}\right)=\parallel e_{m-L}{\parallel }_{P_2}^2$, then (32)${\displaystyle \begin{array}{ccc}\hfill & V\left(e_{m-L}\right)-V\left(e_{m-L-1}\right)\hfill & \hfill \\ \hfill & =\parallel e_{m-L}{\parallel }_{P_2}^2-\parallel e_{m-L-1}{\parallel }_{P_1}^2\hfill \\ \hfill & \le \parallel e_{m-L}{\parallel }_{P_2}^2-\parallel e_{m-L}{\parallel }_{P_1}^2\hfill \\ \hfill & \le \parallel e_{m-L}{\parallel }_{P_2-P_1}^2\hfill \\ \hfill & \le -\parallel e_{m-L}{\parallel }_{Q_2}^2\hfill \\ \hfill & \le -\delta \parallel e_{m-L}\parallel \hfill \end{array}}$ where $\delta =\frac{1}{2}{\lambda }_{min}\left(Q_2\right)r^2$. As a result, Theorem 1 is derived. The ISS analysis result is presented in Eq. (15).

Algorithm

• Give the initial values x₀ and set L = 5.

• Establish T-S fuzzy control system model Eq. (22).

• Solve x_m and z_m in the form of the system.

• Solve Φ_m and Ω_m by formula Eq. (7).

• Obtain the prior prediction ${\overline{x}}_{m-L}$ by formula Eq. (13).

• Calculate the estimation ${\hat{x}}_{m-L\left|m\right|}$ so that ${\hat{x}}_{m\left|m\right|}$ and ${\hat{z}}_{m\left|m\right|}$ using the MHE.

• Set m = m + 1 and go back to step 5.

• Get the estimated value of all state data and end the algorithm.

In the T-S fuzzy control system, two different noise conditions are given to verify the effect of the proposed MHE. The first case is that the noise function is given as the noise gradually decreases over time, and the other case is that the noise is Gaussian noise.

Case 1 (Gaussian noise):

Let the initial condition be zero, that is, x₀ = 0 $\left({\hat{x}}_0=0\right)$, and suppose the disturbance input ω_k is N(0, 1). Under the above-mentioned setting conditions, in order to better illustrate the universality that MHE can achieve the goal, we randomly select Gaussian noise and obtain the estimation result using MHE of the system.

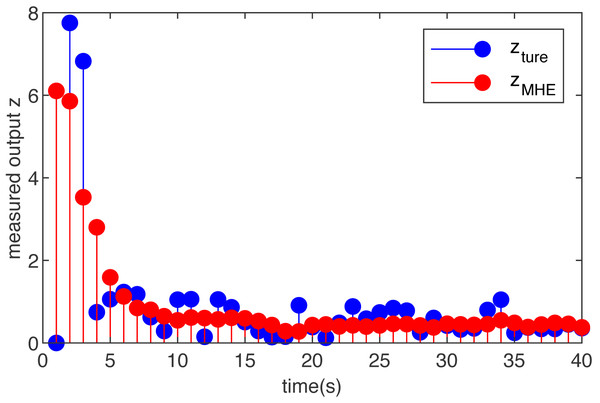
The estimation result of the T-S fuzzy system with Gaussian noise is shown in Fig. 1. Obviously, under the influence of Gaussian noise, the output of the system changes more widely, and the output after adding MHE is more gradual. It shows that when the measured noise satisfies the normal distribution, the performance of estimation is remarkable, and the estimated value curve fluctuates within a smaller range than the true value curve.

Case 2 (non-Gaussian noise):

Let the initial condition x₀ = 0 $\left({\hat{x}}_0=0\right)$, and assume the disturbance input ω_m is (36)${\displaystyle {\omega }_m=\frac{3\ast sin\left(0.85m\right)}{{\left(0.55m\right)}^2+1}}$

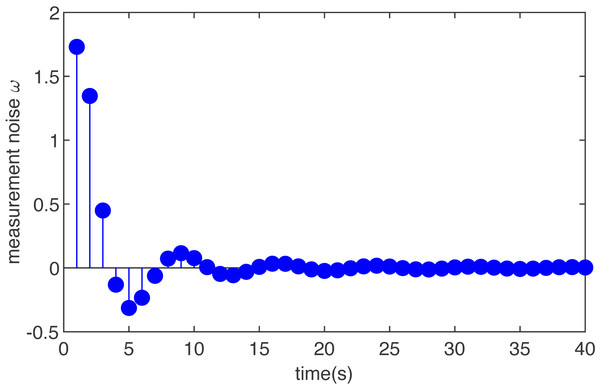
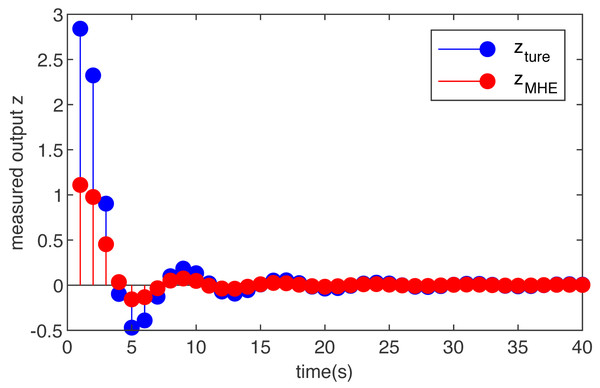
The simulation results are shown in Figs. 2 and 3. Figure 2 is the noise, obviously, the external interference is bounded and non-Gaussian. Figure 3 shows the simulation run for the T-S fuzzy system with the MHE filter. The proposed MHE can effectively counteract the influence of the sine-form noise in the T-S fuzzy system. In this case, the noise decays with time, and the estimation performance of the MHE is most pronounced during the initial period. A clear improvement of the smoothness can be observed for the T-S fuzzy system, which is the result of the MHE filter reducing noise.

Case 3 (non-Gaussian noise):

To make our proposed MHE estimation scheme more convincing in systems with unknown dynamics, we add a case when the noise is uniformly distributed.

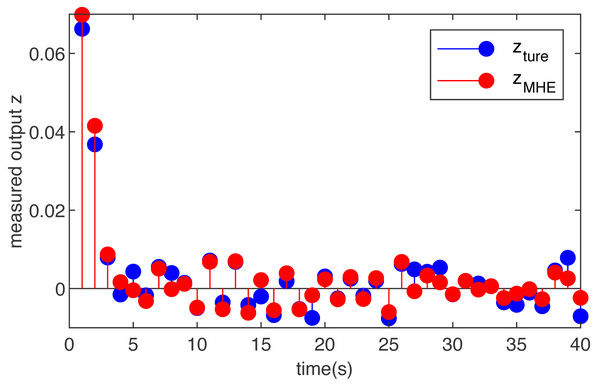
The added noise in this case is shown in Fig. 4 and the effect of the designed MHE filter is shown in Fig. 5. It can be seen from the figure that adding the MHE filter to the T-S fuzzy control model with uniformly distributed noise can make the output smoother. To increase the convincing power, a uniformly distributed noise is added to the designed multi-threaded control system, and MHE filtering is used. It can be seen from the simulation figures that the proposed estimator can work well in systems with unknown factors.

Through the above two kinds of different noise simulations, we find that it is feasible to use MHE to solve the discrete-time filtering problem. The filter based on the MHE method we designed shows a good effect in the T-S fuzzy system with external disturbance, even if the disturbance is non-Gaussian.