Predicting crown width using nonlinear mixed-effects models accounting for competition in multi-species secondary forests

Study site

Guizhou Province is located in the center of the Southeast Asian Karst Region, which is the largest karst area in the world. Karstification is highly developed in this area and the karst types are the most diverse of any karst area globally (Chai et al., 2018). The study took place in the Ziyun Miao and Buyi Autonomous County (105°55′14″–106°29′56″E, 25°21′43″–26°2′30″N) in southwestern Guizhou Province. The region is a typical karst region that has high biodiversity and abundant forest resources, and experiences a mild and humid continental monsoon climate with a mean altitude of 1,185 m, mean annual temperature of 15.30 °C and mean annual rainfall of 1,337.10 mm.

Our study site was the Zhongdong Scenic Area of the Getuanhe National Scenic and Historic Interest Area in Ziyun Miao and Buyi autonomous County, which is a typical karst landform with non-zonal limestone soil and a shallow soil layer. The parent material of the soil is mainly sedimentary rock and carbonate rock. Prior to abandonment in the mid-1980s, cultivated land in this region was extensive and widely distributed. Corn was once the main crop, but after 30 years of reduced human disturbance and reasonable natural recovery, much of the area is now covered by secondary forest and plantation (Chi et al., 2020).

Data collection

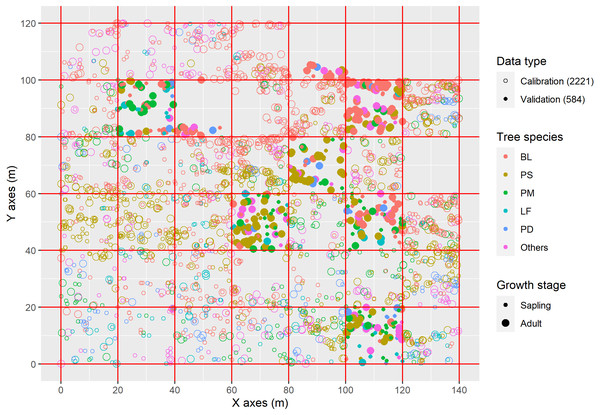
Following field reconnaissance according to the field protocol of the Center for Tropical Forest Science (CTFS) (Condit, 1998), we established an area of 0.168 km² (120 × 140 m) as a permanent sampling plot with typical and low disturbance. The large sample plot was further divided into 42 plots (20 × 20 m) (Fig. 1). In each plot, the altitude, slope gradient and slope aspect were recorded, all woody plants were surveyed and identified, and trees with a diameter at breast height (DBH, at 1.3 m) ≥1 cm were marked. The parameters of species, tree height, DBH, height of crown base, crown width, and crown condition of the trees were determined, and crown width was taken as the arithmetic mean of two crown widths as obtained from measurements of four crown radii in four directions representing two perpendicular azimuths. The geographic coordinates of the trees were recorded with the southwestern corner of the plot taken as the origin (Chi et al., 2020). The trees were roughly divided into two growth stages, saplings (1 cm ≤ DBH < 5 cm) and adults (DBH ≥ 5 cm), and tree species were classified into six groups according to the most numerous species: Betula luminifera (BL), Platycarya strobilace a (PS), Pinus massoniana (PM), Liquidambar formosana (LF), Populus davidiana (PD) and others. Only 39 of 42 plots contained trees, and those 39 plots were randomly divided in two groups: 31 subplots (80%) contained 2,221 trees for calibration data, while validation was performed using 584 trees in the remaining eight plots. The distribution of trees and plots is shown in Fig. 1.

Data analysis

Mixed effect models

The mixed-effects model is a model that includes both fixed- and random-effect variables. In this study, a nonlinear mixed-effects (NLME) modeling framework was used for the hierarchical structure of CW-D data, we set tree species as a random effect. Numerous studies have applied mixed-effects models to describe CW–D relationships and have improved model fit and prediction accuracy. At the plot level, the NLME model of the j th tree height in the i th sample plot was modeled as: (1)${\displaystyle \left\{\begin{array}{c}{\mathrm{CW}}_{ij}=f\left({\varphi }_{ij},u_{ij}\right)+{\varepsilon }_{ij};\hfill \\ i=1,2,3,\dots ,m;j=1,2,3,\dots ,n_i\hfill \end{array}\right.}$ where CW_ijrepresents the CW of the j th tree in the i th plot; m and n_i are the number of plots and observations in the i th plot, respectively; f (.) is a real-valued and differentiable function of a group-specific parameter vector ϕ_ij and covariate vector u_ij; and ɛ_ij is a within-group error, which subjects to a multivariate normal distribution with a mean value vector of 0 and variance–covariance matrix of R. ϕ_ij is given as: (2)${\displaystyle {\varphi }_{ij}=A_{ij}\beta +B_{ij}{b}_i;b_i\sim N\left(0,G\right)}$ where β is the fixed-effect parameter vector; b_i is the random-effect parameter vector of the i th plot, which was assumed to have a multivariate normal distribution with a mean value vector of 0 and variance–covariance matrix of G, A_ij, and B_ij are the incidence matrices of the appropriate dimensions, consisting of 0 or 1. Variance heterogeneity was removed by three frequently used variance functions: the exponential function, power function, and the constant plus power function, and the most effective variance functions was determined by AIC (Fu et al., 2013).

Model evaluation

The following five statistical indices describing model performance were used in this study to evaluate the fit of the CW-D models: Akaike information criterion (AIC), coefficient of determination (R_a²), root mean square error (RMSE), mean absolute prediction error (MAE), and mean absolute percentage error (MAPE). The expressions of these statistical criteria are summarized in Table 5. In general, models with the lowest AIC, RMSE, RMA, MAPE and with the highest R_a² are known to have the best performance.

Statistical analysis

All statistical analyses were performed using R version 4.0.3. Regression was executed using the minpack.lm and nlme package. The figures were drawn and the data were manipulated using the ggplot2 and plyr packages, respectively.

Basic CW model

In the comparison of goodness-of-fit statistics for the 12 CW-D functions fitted to the data for the secondary forests (Table 6), all showed fluctuations within a relatively small range except the Logistic (F11) function, which did not converge, and their parameter estimates were significant at the P < 0.001 level. The Power (F2), Logistic (F10) and Quadratic (F8) functions were found to be superior to other candidate functions during the calibration stage, and the F2 functions performed better than the F8 and F10 during the validation stage. Therefore, the Power (F2) function was selected as the basic CW model in this study. It is expressed as follows: (3)${\displaystyle {\mathrm{CW}}_{ij}=0.861{\mathrm{D}}_{ij}^{0.620}+{\varepsilon }_{ij}}$ where CW_ij and D_ij represent the crown width (m) and DBH (cm) of the j th tree in the i th plot, respectively, and ɛ_ij is the error term.

Generalized CW model

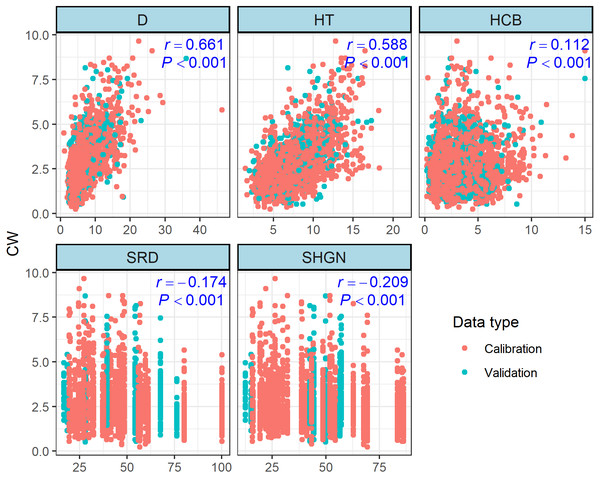
To avoid the effects of over-parameterization and collinearity in the estimated models, we selected variables with graphical exploration of the data and examination of the correlation statistics, and only those variables displaying a significant contribution to crown width variation were retained (Fig. 2). The selected variables are: tree height (TH), height of crown base (HCB), and sum of relative dbh (SRD) and sum of hegyi index (SHGN) were identified as the optimum distance-independent competition indices and distance-independent competition indices, respectively. Correlation analysis showed that these variables were significantly correlated with the CW (Fig. 3). Therefore, the function was expanded as follows (F2): (4)${\displaystyle {\mathrm{CW}}_{ij}=\left(\varphi 1+\varphi 3SR{D}_i/SHG{N}_i+\varphi 4T{H}_{ij}+\varphi 5HC{B}_{ij}\right)D_{ij}^{\varphi 2}+{\varepsilon }_{ij}}$ where TH_ij, HCB_ijrepresent the tree height (m), height of crown base (cm) of the jth tree in the ith plot, SRD_i/SHGN_i represents the distance-independent/distance-dependent competition index of the i th plot; ϕ1, ϕ2, ϕ3, ϕ4, and ϕ5 are formal parameters. The spatially non-explicit and spatially explicit generalized CW models were obtained and are displayed in Eqs. (5) and (6), respectively. The goodness-of-fit statistics of the generalized CW models are shown in Table 6. (5)${\displaystyle {\mathrm{CW}}_{ij}=\left(0.901-0.001{\mathrm{SRD}}_i+0.066{\mathrm{TH}}_{ij}-0.042{\mathrm{HCB}}_{ij}\right){\mathrm{D}}_{ij}^{0.441}+{\varepsilon }_{ij}}$ (6)${\displaystyle {\mathrm{CW}}_{ij}=\left(0.995-0.003{\text{SHGN}}_i+0.065{\mathrm{TH}}_{ij}-0.038{\mathrm{HCB}}_{ij}\right){\mathrm{D}}_{ij}^{0.434}+{\varepsilon }_{ij}}$

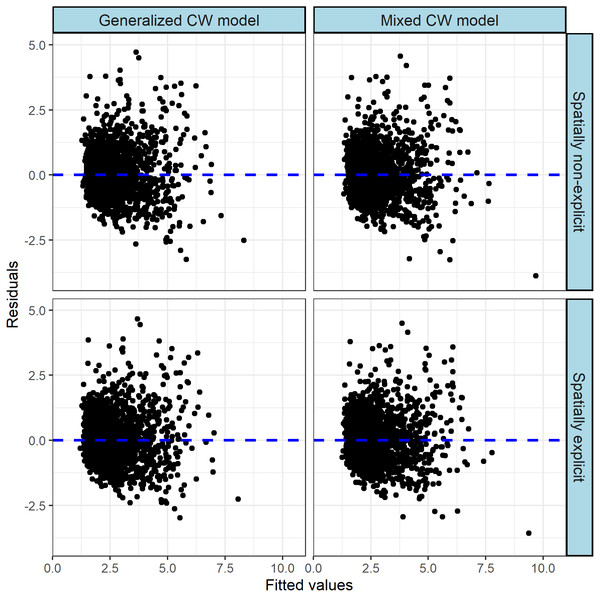
The multiple model performance criteria confirmed that the both generalized CW models Eqs. (5) and (6) show a substantial improvement compared with basic CW model Eq. (3) when the covariates are added. Meanwhile, the spatially explicit generalized CW-D model Eq. (6) performed better than spatially non-explicit model Eq. (5) (Table 7). Figure 4 also demonstrates that heteroscedasticity in the residuals was reduced by generalized models, and heteroscedasticity in the residuals for the spatially explicit generalized model was smaller than that for the spatially non-explicit generalized model.

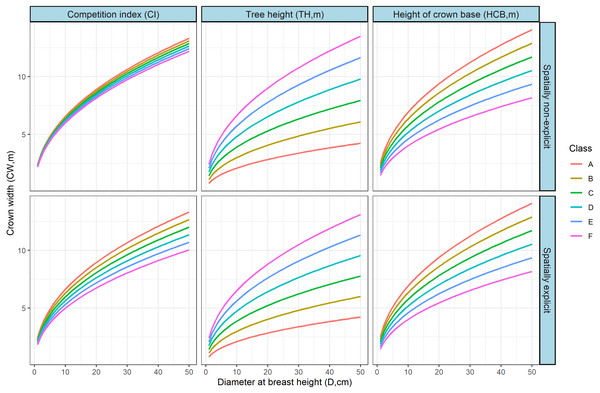
The effects of HCB, TH and CI on the CW-D relationship were simulated by CW-D curves (Fig. 5) using the generalized CW-D model (Eqs. (5) and (6)). The variables of interest were roughly divided into six equal intervals, and the simulation demonstrated that the HCB, TH, and CI had more considerable contribution to the CW-D models, the differences of CW were greater with the increase of DBH, and each of HCB, TH, and CI significantly affected the initial CW-D relationship.

Mixed-effects CW model

There are 31 potential different combinations of random effects for Eq. (4) considering all independent variables and the intercept in the generalized model when species is included as random effect. Fitted to the data, 25 of the mixed-effects model alternatives reached convergence, with Eq. (7) yielding the smallest AIC (AIC = 5645) for the spatially explicit mixed-effects model, and 23 of the mixed-effects model alternatives reached convergence, with Eq. (7) yielding the smallest AIC (AIC = 5584) for the spatially non-explicit mixed-effects model. (7)${\displaystyle {\mathrm{CW}}_{ij}=\left[\varphi 1-\varphi 3SR{D}_i/SHG{N}_i+\varphi 4T{H}_{ij}+\left(\varphi 5+u{5}_i\right)HC{B}_{ij}\right]D_{ij}^{\left(\varphi 2+u{2}_i\right)}+{\varepsilon }_{ij}}$ where ϕ1 − ϕ5 are fixed-effects parameters, u2_i, u5_i are random-effects parameters generated by tree species. After the determination of parameter effects and error variance–covariance structure, the final mixed-effects models were proposed in Eqs. (8) and (9). The residual plots and goodness-of-fit statistics are shown in Fig. 4 and Table 5, respectively. (8)${\displaystyle {\mathrm{CW}}_{ij}=\left[0.967-0.001SR{D}_i+0.059T{H}_{ij}+\left(-0.028+u{5}_i\right)HC{B}_{ij}\right]D_{ij}^{0.417+u{2}_i}+{\varepsilon }_{ij}}$ where ${\displaystyle {\mathrm{u}}_i=\left[\begin{array}{c}\hfill u{2}_i\hfill \\ \hfill u{5}_i\hfill \end{array}\right]\sim N\left\{\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\psi =\left(\begin{array}{cc}\hfill 0.002\hfill & \hfill -0.0009\hfill \\ \hfill -0.0009\hfill & \hfill 0.0004\hfill \end{array}\right)\right\},{\varepsilon }_{ij}\sim N\left(0,R_{ij}=0.733G_{ij}^{0.5}{I}_{ni}{G}_{ij}^{0.5}\right),var\left({\varepsilon }_{ij}\right)=0.733D_{ij}^{-3.012}}$ and (9)${\displaystyle {\mathrm{CW}}_{ij}=\left[1.057-0.003SHG{N}_i+0.057T{H}_{ij}+\left(-0.022+u{5}_i\right)HC{B}_{ij}\right]D_{ij}^{\left(0.410+\mathrm{u}{2}_i\right)}+{\varepsilon }_{ij}}$ where ${\displaystyle {\mathrm{u}}_i=\left[\begin{array}{c}\hfill u{2}_i\hfill \\ \hfill u{5}_i\hfill \end{array}\right]\sim N\left\{\left[\begin{array}{c}\hfill 0\hfill \\ \hfill 0\hfill \end{array}\right],\psi =\left(\begin{array}{cc}\hfill 0.002\hfill & \hfill -0.001\hfill \\ \hfill -0.001\hfill & \hfill 0.0005\hfill \end{array}\right)\right\},{\varepsilon }_{ij}\sim N\left(0,R_{ij}=0.713G_{ij}^{0.5}{I}_{ni}{G}_{ij}^{0.5}\right),var\left({\varepsilon }_{ij}\right)=0.713D_{ij}^{-2.722}.}$

We found that the both mixed-effects CW models Eqs. (8) and (9) show a substantial improvement compared with corresponding generalized CW model Eqs. (5) and (6) when species is included as random effect. We found that the addition of random parameters in could significantly improve the predictive ability for crown width. Meanwhile, the spatially explicit mixed CW-D model Eq. (9) performed better than the spatially non-explicit model Eq. (8) (Table 5).

Relationship between SHGN and SRD

Considering the importance of competition for crown width development and modelling, SHGN and SRD were selected for the analyses of linear regression to quantify competition. SHGN had a significant positive linear correlation with SRD (Fig. 3, R² = 0.943 and P < 0.001).