Optimization of change in epicardial fat thickness for obese patients who lost weight via the bariatric surgery method using central composite and Box-Behnken experimental designs

Calculation of stationary points

The determination of the components in the quadratic response surface method depends on the size of the coefficients given in the regression equation. The steps to be followed for the calculation of stationary points are as follows.

(i) A quadratic response surface model is estimated with the help of the data obtained from the experiment [experimental].

(ii) Partial derivatives are taken for each of the factors included in a model and equalized to zero. (2)${\displaystyle \frac{\partial \hat{Y}}{\partial {\chi }_1}=\frac{\partial \hat{Y}}{\partial {\chi }_2}=...=\frac{\partial \hat{Y}}{\partial {\chi }_j}=0}$

(iii) Equation (2) system of equations obtained in step (ii) is solved. A value will be obtained for each factor. These values are put into place in the model and the estimated value of dependent variable for the stationary points is obtained.

It is possible to obtain the stationary points with the help of matrices. If the given model is expressed in matrices; (3)${\displaystyle \hat{Y}=b_1+x^{\prime }b+x^{\prime }\hat{B}\chi }$

In Eq. (3); b₁ is the model constant, b is estimate of the linear model coefficients, and $\hat{B}$ is the estimate of the quadratic model coefficients.

In addition; (4)${\displaystyle x^{\prime }=\left[x_1,\dots ,x_j\right]}$

$\hat{B}$ is a symmetric matrix with k x k dimensions. (5)${\displaystyle \hat{B}=\left[\begin{array}{ccccc}\hfill b_{11}\hfill & \hfill \frac{1}{2}{b}_{12}\hfill & \hfill \hfill & \hfill \hfill & \hfill \frac{1}{2}{b}_{1q}\hfill \\ \hfill \frac{1}{2}{b}_{12}\hfill & \hfill \frac{1}{2}{b}_{22}\hfill & \hfill \hfill & \hfill \hfill & \hfill \frac{1}{2}{b}_{2q}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill \frac{1}{2}{b}_{1q}\hfill & \hfill \frac{1}{2}{b}_{2q}\hfill & \hfill \hfill & \hfill \hfill & \hfill b_{qq}\hfill \end{array}\right]}$

Stationary points can be obtained from Eq. (6); (6)${\displaystyle x_S=\frac{1}{2}{\hat{\beta }}^{-1}b}$

If we substitute the stationary points in the main equation, Eq. (7) will be obtained; ${\displaystyle {\hat{Y}}_S=b_0+x_S^{\prime }b+x_S^{\prime }\hat{B}{x}_S}$ (7)${\displaystyle {\hat{Y}}_S=b_0+\frac{1}{2}{x}_S^{\prime }b}$ ${\hat{Y}}_S$ is the value of the response variable estimated from the stationary point (Doğan & Okut, 2003; Schmidt & Launsby, 1992; Lucas, 1994; Lawson & Madrigal, 1994).

Structure of stationary point (Canonical analysis)

When a quadratic equation is found to be adequate, the canonical analysis is applied to decide about the location and structure of stationary points in a quadratic equation. The signs of the eigenvalues obtained with the help of $\hat{B}$ matrix determine the stationary point structure. For this, it is possible to write a new equation containing canonical variables. (8)${\displaystyle \hat{Y}={\hat{Y}}_S+\sum _{j=1}^k{\lambda }_j{W}_j^2}$ In Eq. (8), λ₁, λ₂, …, λ_k show the eigenvalues to be obtained from the vector $\hat{\beta }$, while W₁, W₂, …, W_k denote the “canonical variables”. It can be possible to understand the properties of the stationary points obtained with the help of Eq. (8).

(i) If λ₁, λ₂, …, λ_k eigenvalues are all negative, the stationary point represents the maximum point.

(ii) If λ₁, λ₂, …, λ_k eigenvalues are all positive, the stationary point shows the minimum point.

(iii) If the signs of λ₁, λ₂, …, λ_k eigenvalues are mixed, the stationary point indicates the “saddle point” (Doğan & Okut, 2003; Lawson & Madrigal, 1994; Alexander, 1997).

Initially, CCD and BBD experimental designs used in patient selection were created with the MINITAB package program (Tables 1 and 2). The statistical packages of Minitab® (Minitab Statistical Software, State College, Pennsylvania, USA) were used for routine data analysis and for both design and analysis of the central composite (CCD) and the Box–Behnken design (BBD).

Central composite experimental design

The Central Composite experimental design (CCD) is one of the most popular methods for generating a quadratic response level model. The CCD consists of a combination of 2^k two-level factorial experiments with 2k number of axis points or star points, where “k” is the number of factors. It also contains n_c center points. The factors in the model should be at least two levels. The placement of the axis points in the experimental design [set-up] is given in Table 1. While the main effects of the quadratic model to be established and first-order interaction effects are obtained from 2^k experiments, the curvilinearity of the system is tested with the help of the center points and the quadratic terms in the model are estimated with the help of the axis points (Alexander, 1997; Doğan & Okut, 2003; Schmidt & Launsby, 1992; Lawson & Madrigal, 1994; Özler, 2006).

Box-Behnken experimental design

These experimental design, introduced by Box and Behnken in 1980, are an effective method for constructing the quadratic response surfaces model. It is a method built on balanced incomplete block experiments. The factors to be included in the model must be at least three levels. If we try to explain the structure of the experiment with the help of a experimental design with three factors; in the Box-Behnken experimental design, while the value of one of the factors is fixed at the central value, the combinations for all levels of other factors are applied (Alexander, 1997; Doğan & Okut, 2003; Myers & Montgomery, 2002; Montgomery, 2001; Tekindal et al., 2012). As can be seen in Table 2, firstly the level of C factor is fixed, the combinations of all levels of A and B factors are applied and then the same operations are applied by fixing the levels of B and A factors in the center, respectively. In the last columns of the design matrix, there are the center point values.

The smallest is the best

The aim is to reach the minimum response variable. When the aim is to minimize the response variable, the target value for the Taguchi response variable is treated as if it is zero. The squared loss function is defined as $E_2{\left(y-0\right)}^2$. (9)${\displaystyle SN{R}_s=-10log\sum _{i=1}^n\frac{y^2}{n}}$ The above ratio is a ratio used to find x value that gives the levels of the control variables which minimize the expected squared loss error E₂y².

${\sum }_{i=1}^n$: the sum of the values in the outer zone of n response variables. The SNR value will be calculated for each inner zone point.

The largest is the best

The aim is to reach the maximum response variable. It is handled in a similar way to “the smallest is the best” case. The value of $\frac{1}{y}$ is substituted for the value of y in Equation 8.2 [Eq. (9)].

The expected squared loss error is obtained as follows; (10)${\displaystyle E_2{\left(\frac{1}{y}\right)}^2}$ and (11)${\displaystyle SN{R}_s=-10log\sum _{i=1}^n\frac{1∕y^2}{n}}$

The target is the best

In this method, the aim to find χ value that gives the levels of the control variables that make the response variable the target value. In this case, two different SNRs are considered. Which SNR to use depends on the structure of the system. If the mean and variance of the response variable can be changed independently, one or more response variables can be used to remove the bias, according to Taguchi. These adjustment [manipulated] variables allow the researcher to change the mean without changing the variance. This analysis has two stages. First, the adjustment factors that enable the response variable to reach the target value are selected, and then the levels of other control factors that minimize the SNR value are determined. In this case, the expected squared loss error is obtained as follows (Tekindal et al., 2012; Tekindal & Kaymaz, 2018; Tekindal et al., 2014; Bayrak, Özkaya & Tekindal, 2010); (12)${\displaystyle E_2{\left(y-t\right)}^2}$ and (13)${\displaystyle SN{R}_{T1}=-10log{s}^2}$ s² is the sample variance calculated over the experimental points located in the outer zone of the cross zone, and determined with the following equation. (14)${\displaystyle s^2=\frac{\sum _{i=1}^n{\left(y_i-\bar{y}\right)}^2}{n-1}}$ When the factor levels that maximize the SNR value are applied, the value of the response variable will reach the target value.

For cases where the standard error of the response variable is related to the mean values, a different SNR value is proposed. This is a value that can be best applied in cases where the relationship is linear (Tekindal et al., 2012; Tekindal & Kaymaz, 2018; Tekindal et al., 2014; Bayrak, Özkaya & Tekindal, 2010). (15)${\displaystyle SN{R}_{T2}=-log\left(\frac{{\bar{y}}^2}{s^2}\right)}$

Data set

From the results of these experiments, firstly, the point belonging to the factor levels providing the highest efficiency is estimated; then it is tried to determine the point in question (the combination that provides the highest efficiency), with the way to reach where the actual optimum point is or by making the steepest increase from the second-order [quadratic] by using the coefficients of the first-order response surface function of the first experimental results (the steepest ascent method).

The study data belong to 40 obese patients who lost weight through the Bariatric Surgery between February 2015 and December 2016. The values of BMI, Age and HOMA for the obese patients who lost weight through the Bariatric Surgery were evaluated in three categories and at three levels. Data from a subset of patients from Altin et al., published in 2016, were used in the current study (Altin et al., 2018). “Verbal informed consent” was obtained from the participants. The response variable was determined as the ΔEFT. The experimental design was set up before starting the study, and the study data were identified in accordance with the experimental design. Informed consent was obtained from the study participants.

In the study, after the CCD and BBD designs were determined, patients were selected for 40 subjects who were admitted to the hospital and met the relevant criteria. The age of 40 subjects is 40.45 ± 11.30 minimum age 18 and maximum 66 years. Also, the BMI is 45.95 ± 7.51 minimum 35.06, maximum 64.47. The pre-experimental HOMA values are 8.09 ± 6.52 minimum 2.72 and maximum 38.40. In the study, weights were measured in kg, 2 digits after the comma, before and after the patients were only wearing surgical gowns. Within the scope of the study per protocol, all patients were followed during the 180-day follow-up period and the final measurements were taken. The study was carried out by providing all the assumptions of CCD and BBD experimental designs. The target is best algorithm was used in our study.

The division into three categories for age, BMI and HOMA values in Table 3 was made by field experts and co-authors within the framework of clinical observation.

Measurement of epicardial fat thickness

EFT can be identified as the echo-free space between the free [outer] wall of the myocardium and the visceral layer of the pericardium. It is measured by the standard transthoracic 2D echocardiography (Vivid S5 ultrasound machine, GE, Healthcare, Horten, Norway) in the parasternal long-axis views of three cardiac cycles at the end of the diastole and perpendicular to the right ventricular free wall as previously described (Altun, 1998; Kul, 2004; Mead & Pike, 1975). The same investigators, who were blinded to all clinical data of the patients, performed all measurements. After that, the data were digitally stored and reviewed by a senior echocardiographer in order to avoid the inter-reader variability.

As can be seen in Table 4, the interaction effects of variables of Age and BMI, Age and HOMA, and BMI and HOMA [on ΔEFT] were found to be significant (p; 0.041, 0.031 and 0.026, respectively). According to these results, the optimum ΔEFT combinations were determined by drawing the contour and response plots, and the model was expressed as specified in Eq. (16). The R² value of the model was found to be 87.75%. (16)${\displaystyle \Delta \mathrm{EFT}=2.03+0.0198\mathrm{Age}+0.013\mathrm{BMI}+0.0078\mathrm{HOMA}-0.000481\mathrm{Age}\ast \mathrm{Age}-0.00028\mathrm{BMI}\ast \mathrm{BMI}-0.000282\mathrm{HOMA}\ast \mathrm{HOMA}+0.000168\mathrm{Age}\ast \mathrm{BMI}+0.000055\mathrm{Age}\ast \mathrm{HOMA}+0.000221\mathrm{BMI}\ast \mathrm{HOMA}\mathrm{The}{R}^2\mathrm{of this model was}0.88}$

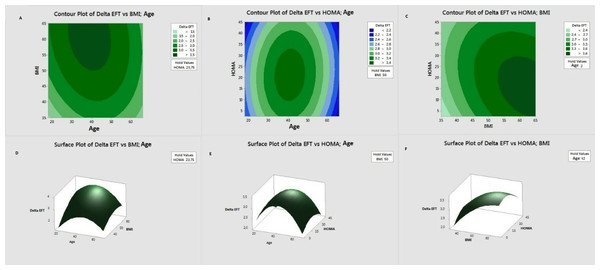
When Fig. 1 was examined, as a result of CCD analysis, the optimum ΔEFT was determined as ΔEFT = 2.571, where Age = 30.52, BMI = 45.30, HOMA = 34.62.

While planning the BBD design, it was established as three factors and three central points.

When Table 5 was examined, the interaction effects of variables of Age and BMI, Age and HOMA, and BMI and HOMA [on ΔEFT] were found to be significant (p; 0.043, 0.040 and 0.022, respectively). According to these results, the optimum ΔEFT combinations were determined by drawing the contour and response plots, and the model was expressed as specified in Eq. (17). The R² value of the model was found to be 91.27%. (17)${\displaystyle \Delta \mathrm{EFT}=-7.72+0.1718\mathrm{Age}+0.245\mathrm{BMI}+0.0599\mathrm{HOMA}-0.001746\mathrm{Age}\ast \mathrm{Age}-0.00166\mathrm{BMI}\ast \mathrm{BMI}-0.000766\mathrm{HOMA}\ast \mathrm{HOMA}-0.000653\mathrm{Age}\ast \mathrm{BMI}+0.000173\mathrm{Age}\ast \mathrm{HOMA}-0.000690\mathrm{BMI}\ast \mathrm{HOMA}{R}^2\mathrm{of the model was 0.91}}$

When Fig. 2 was examined; as a result of the BBD analysis, the optimum ΔEFT = 3.756 was determined, where Age =38.36, BMI =63.18, HOMA =14.95.

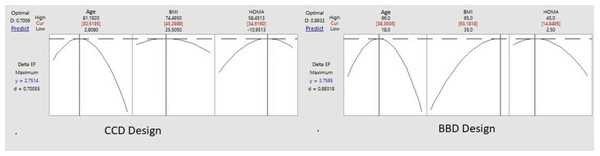
Figure 3 shows clear optimal differences between CCD and BBD designs.